Вычисление жордановой нормальной формы линейного преобразования A:LàLи соответствующего жорданова базиса в случае dim L=3, страница 2

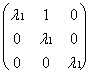
Случай 3в. Геом. крат. l1 = 1. Тогда в ж.н.ф. л.п. A будет одна клетка с l1 на главной диагонали, которая совпадёт со всей ж.н.ф.:

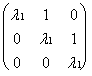
Замечание 1. Рассматривая эти случаи, мы обнаружили, что для вычисления ж.н.ф. матрицы третьего порядка (без соответствующего жорданова базиса) достаточно найти собственные значения и их алгебраические и геометрические кратности. Легко видеть, что для матрицы четвёртого порядка это уже не так.

Пример 1. Пусть [A] = .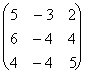

Тогда FA (l) = – (l-1)(l-2)(l-3), т.е. l1  = 1, l2 = 2, l3=3.

1)  Ищем соб. Векторы, соответствующие l1  = 1.

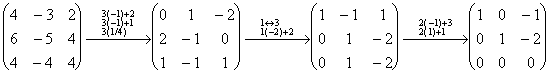
Получена матрица специального ступенчатого вида. Общее решение однородной СЛАУ .

2)  Делаем то же для l2 = 2.

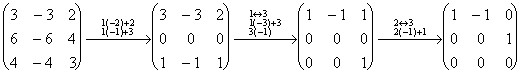
Общее решение

3)  Делаем то же для l3=3.

 
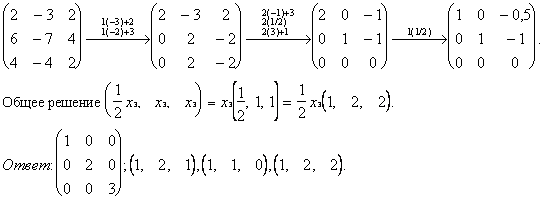
При желании можно сделать проверку для себя:

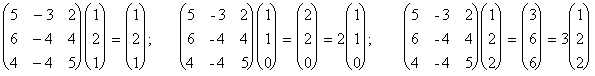
Пример 2а. Пусть [A] = .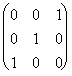

Тогда FA (l) = –, т.е. l1  = 1, l2 = -1.

1)  Ищем собственные векторы, соответствующие l1  = 1.

 

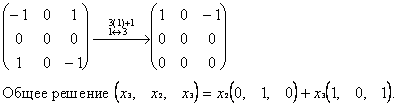
2)  Делаем то же для l2 = -1.

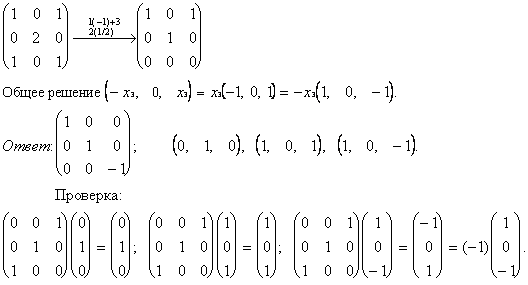
Пример 2б. Пусть [A]=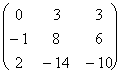

Тогда FA (l) = , т.е. l1  = -1, l2 = 0.

1)  Для собственного значения l1  = -1 ищем начальные базисы подпространств Li (i = =1, 2,...).

Сначала найдём базис подпространства L1  = .

Начальный базис подпространства L1 состоит из одного вектора (3, 3, -4). Видим, что геом. крат. l1  = 1 и мы имеем случай 2б.

Теперь найдём базис подпространства L2 =

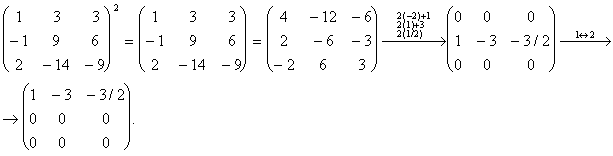
Общее решение 

Строим начальный базис подпространства L2, дополняя базис подпространства L1 (3, 3, -4) до базиса подпространства L2 векторами из базиса (3, 1, 0), (3, 0, 2). Можно это сделать, например, так: (3, 3, -4), (3, 1, 0) (эта система векторов, очевидно, линейно независима). Поскольку dim L2 = 2 = алг. крат. l1  = dim , то L2 = , т.е. L3 не надо рассматривать.

Высоты корневых векторов из построенного начального базиса подпространства L2 таковы: (3, 3, -4) высоты 1 (он принадлежит L1; (3, 1, 0) высоты 2 (он принадлежит L2\ L1). Из корневого вектора (3, 1, 0) высоты 2 вытаскиваем серию: u1  = (3, 1, 0);

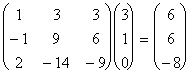, т.е. u2 = (6, 6, -8).   Обратная серия (6, 6, -8), (3, 1, 0) является базисом подпространства L2 = .

2)Разберёмся теперь с собственным значением l2 = 0. Так как геом крат. l2 = алг. крат. l2=1, то  = и остаётся найти соответствующие собственные векторы.

.

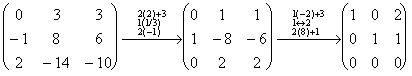Общее решение