Адаптивные системы управления. Принципы построения СНС (беспоисковых), страница 2

- Метод ЛСП с пересчетом, - Локальный случайный поиск по наилучшей пробе, - ЛСП по статическому градиенту, - Глобальный поиск с независимым выбором плотности распределения пробных шагов.

Достоинство: требует меньшего объема информации. Недостаток: быстродействие хуже, точность хуже (в некоторых случаях).

Инвариантные системы.

Задача всех АСР заключается в следующем: необходимо точно воспроизводить задание на выходе системы.

В статическом режиме точность системы можно повысить , увеличивая коэффициент передачи системы , либо увеличивая порядок астатизма системы. В свою очередь повышение коэффициента передачи системы приводит к уменьшению запаса устойчивости и увеличению колебательности, т.е. точность в переходном режиме уменьшается. Это противоречие между точностью в переходном режиме и установившемся необходимо решить . Оно решается с помощью введения управляющего воздействия по возмущению.

Система, у которой использовано два принципа управления по заданию и по возмущению называется комбинированной.

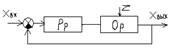
Z-помеха, учитывается, идет на вход регулятора .

 Инвариантность заключается в следующем: В системах стабилизации необходимо добиться независимости выходной величины от возмущающего воздействия (помехи ).

 В следящих системах необходимо добиться независимости сигнала ошибки от задающего воздействия .

 Математическое определение условий независимости получили название теории инвариантности .

Теоремы Лапласа.

1) Теорема подобия f(at)=F(p/a)/a

2)Теорема смещения. e^at*f(t)÷F(p-a)

3)Теорема запаздывания. f(t-τ)÷e^-pτ·F(p)

4)Дифференцирование оригинала.

fⁿ(t)=pⁿ ·F(p)-p^n-1 ·F(0)-p^n-2 ·F^/(0)-…-F^n-1(0)

5) Интегрирование оригинала. ∫f(τ)dτ от0доt÷F(p)/p

6)Дифференцирование изображения. tⁿ·f(t) ÷ (-1)ⁿFⁿ(p)

6)Теорема о нач. знач-ии ориг-ла. lim pF(при p→∞)=f(0)

7) Интегрирование изображения f(t)/t÷∫F(p)dp от0до∞.

8) Теорема умножения. F(p)Ф(p)÷∫f(τ)φ(t-τ)dτ от0доt

9) Интеграл Дюамеля. pF(p)Ф(p)÷f(t)·φ(0)+∫f(τ)·φ’(t-τ)dτ от0доt

Дискретное преобразование Лапласа. Теоремы:

1) Теорема линейности. Если реш. ф-я f[n] -линейная комбинация реш-тых ф-ий, то изображение линейной комбинации решетчатых функций равно линейной комбинации их изображений.

2) Теорема сдвига. f[n-k]÷e^-qk F*(q).

3) Теорема смещения. e^an·f[n]÷F*(q-a)

4) Теорема об изображении разностей.

Первую разность реш. Ф-иинаходят по формуле: ∆f[n]÷f[n+1]-f[n],применив теоремы линейности и сдвига, получим ∆f[n]÷e^q [F*(q)-f[0]]-F*(q). Для второй разности реш. функции ∆²f[n]÷f[n+1]-∆f[n] получим

5) Теорема об изображении суммы.

6) Теорема об умножении изображений (теорема свертывания в вещественной области). Если реш. ф-ии f[n] и f[r], то свёрткой будет их сумма, т.е. операции свертывания решетчатых функций соответствует простое перемножение изображений.

7) Теорема о начальном значении оригинала решетчатой функции. f[0,ε]=lim F*(q,ε) при q→∞. Т.е. нач знач-е реш ф-ии равно ее дискр изоб-ию при q→∞.

8) Теорема о конечном значении оригинала решет. функции. lim f[n,ε] при n→0 = lim (e^q -1)F*(q,ε) при q→0

9) Теорема о дифференцировании изображения дискретного преобразования Лапласа.

n[m] / m!=(n(n-1)…(n-m+1)) / m! ÷ e^q / ((e^q -1)^m+1)

Разностные ур-я. (1 и 2-го порядков):

n÷e^q/(e^q -1)², n²÷e^q (e^q +1) / (e^q -1)³.