Общая постановка задачи оптимизации. Численные методы поиска безусловного экстремума. Линейное программирование: симплекс-метод и его применение для решения задач оптимизации, страница 2

Находят значения G в точках Х₃ и Х₄ , сравнивают значения. Предположим интервал неопределенности смещен вправо , в результат берем отрезок [Х₃; Х₂].

Внутри него находят новую пару значений Х₅ и Х₆ и т. д.

До тех пор, пока длина оставшегося интервала:

N – количество заданных шагов поиска экстремума.

Алгоритм метода квадратичной интерполяции

            Шаг 1.  Задать начальную точку x1, величина шага Dx > 0, e1 и e2 – малые положительные числа, характеризующие точность.

            Шаг 2. Вычислить x2 = x1 + Dx.

            Шаг 3. Вычислить f(x1)=f1 и f(x2)=f2.

            Шаг 4. Сравнить f(x1) с f(x2):

а) если f(x1)>f(x2), положить x3 = x1 + 2Dx;

б) если f(x1)≤ f(x2), положить x3 = x1 – Dx.

Шаг 5. Вычислить f(x3)=f3.

            Шаг 6. Найти Fmin{f1, f2, f3}, xmin = xi, f(xi) = Fmin.

            Шаг 7. Вычислить точку минимума интерполяционного полинома, построен-ного по трем точкам:

 

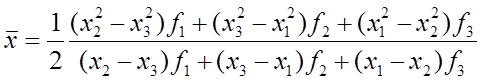и f(x)

Если знаменатель в формуле на некоторой итерации обращается в нуль, то результатом интерполяции является прямая. В этом случае рекомендуется обозначить x1 = xmin и перейти к шагу 2.

            Шаг 8. Проверить выполнение условий окончания: 

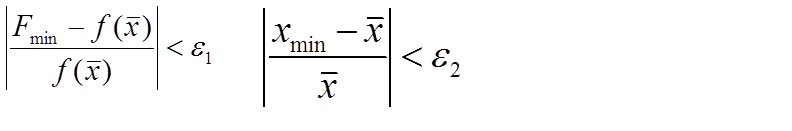
3 Численные методы поиска безусловного экстремума: методы первого порядка.

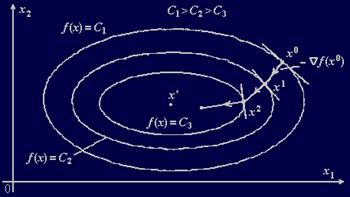
Метод градиентного спуска с постоянным шагом

Надо построить последовательность точек {xk}, k = 0, 1, …, таких, что f(xk+1)<f(xk),
k = 0, 1, …. Точки последовательности {xk} вычисляют по правилу

 

где точка x0 задается самостоятельно; Ñf(xk) – градиент функции f(x), вычисленный в точке xk; величина шага tk задается самостоятельно и остается постоянной до тех пор, пока функция убывает в точках последовательности, проверка выполнения условия

                                                

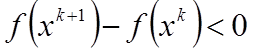
Построение последовательности {xk} заканчивается в точке xk, для которой

||Ñf(xk)|| < e1, где e1 – заданное малое положительное число или k≥M, где M – предельное число итераций, или при двукратном одновременном выполнении двух неравенств

||xk+1 – xk|| < e2, | f(xk+1) – f(xk) | < e2 ,

где e2 – малое положительное число.

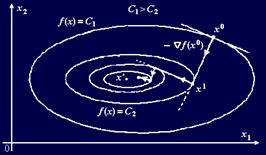
Метод наискорейшего градиентного спуска

Надо построить последовательность точек {xk}, k = 0, 1, …, таких, что

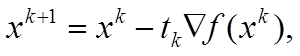 f(xk+1)<f(xk), k = 0, 1, …. Точки последовательности {xk} вычисляют по правилу

где точка x0 задается самостоятельно; величина шага tk определяется для каждого значения k из условия

 

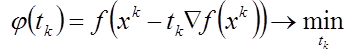Проверяется необходимое условие минимума:

 

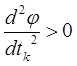а потом проверяется достаточное условие.

Метод покоординатного спуска

Надо построить последовательность точек {xk}, k = 0, 1, …, таких, что

 f(xk+1)<f(xk), k = 0, 1, …. Точки последовательности {xk} вычисляют :

 

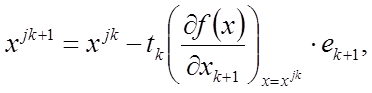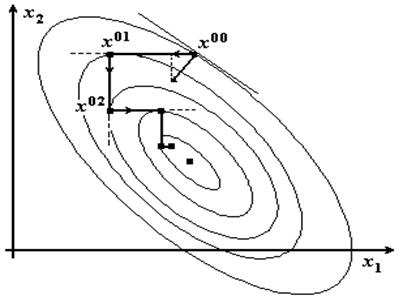
где j – номер цикла вычислений, j = 0, 1, 2, …; k – номер интеграции внутри цикла, k = 0, 1, …, n–1; ek+1 – единичный вектор, (k+1)-я проекция которого равна 1; точка x00 задается нами, величина шага tk выбирается из условия

 

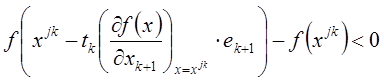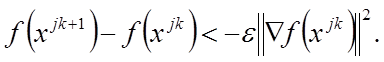Если выбранное условие при текущем tk не выполняется, шаг уменьшается вдвое и точка

 

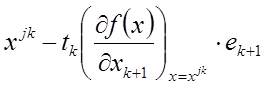вычисляется заново. При фиксированном j за одну итерацию с номером k изменяется только одна проекция точки xjk, имеющая номер k + 1, а в течение всего цикла с номером j, т.е. начиная с    k = 0 и кончая k = n – 1, изменяются все n проекций точки xj0.

После этого точке xjn присваивается номер xj+1,0 и она берется за начальную точку для вычисления в j+1 цикле. Расчет заканчивается в точке xjk при выполнении по крайней мере одного из трех критериев окончания счета:
||Ñf(xjk)||<e1, или j ≥ M, или двукратного выполнения неравенств ||xjk+1 – xjk|| < e2, 
| f(xjk+1) – f(xjk) | < e2 .

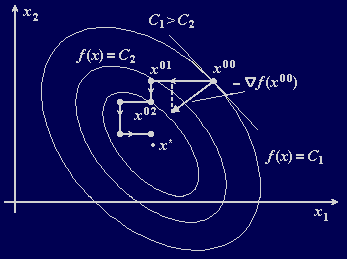
Метод Гаусса-Зейделя

Надо построить последовательность точек {xk}, k = 0, 1, …, таких, что

 f(xk+1)<f(xk), k = 0, 1, …. Точки последовательности {xk} вычисляют по правилу

 

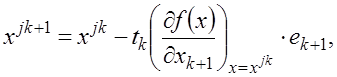где j – номер цикла вычислений, j = 0, 1, 2, …; k – номер интеграции внутри цикла, k = 0, 1, …, n–1; ek+1 – единичный вектор, (k+1)-я проекция которого равна 1; точка x00 задается пользователем, величина шага tk выбирается из условия

 

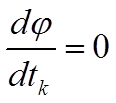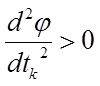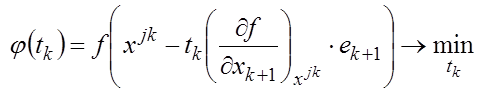4 Линейное программирование: симплекс-метод и его применение для решения задач оптимизации.

Систему ограничений записывают в виде равенств: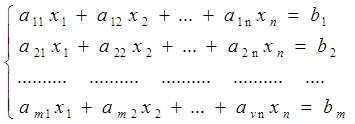

х_j≥0, j=1,2…n.

Целевую функциюю F приводят к виду F→min.

2)Выбирают m – базисных переменных и выбирают их через (n-m) свободных переменных, получают 1-й базис, в котором матрица коэффициентов при базисных переменных единичная, получают первое базисное решение.

3)Если среди коэффициентов при свободных переменных целевой функции  есть хотя бы один отрицательный, можно улучшить решение. Если отрицательных несколько, то выбирают наибольшую по модулю, тогда столбец с индексом j будет ведущим.

4)Выбирают ведущую строку из условия min-го отношения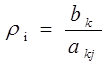  

Коэф-т вычисляют только для тех строк для которых коэф-ты а_ij  положительны. Если коэф-т а_ij<0, то для него не вычисляется.

5)Каждый элемент ведущей строки делят на разрешающий элемент так, чтобы коэффициент при переменной х_j был = 1, образуется новая строка, которая записывается на старое место в новой таблице.

6)В остальных строках исключают переменную х_j, добиваясь, чтобы во всех строках коэффициенты при этих переменных были =0, и  переменная  х_j входит в базис, а некоторая переменная х_i выходит из базиса.

7)Определяем новое базисное решение и новое значение F. Вычисляют вектор относительных оценок, (-строку).

8)Проверяют полученное решение на оптимальности. Если решениее не оптимально, т.е. в -строке есть отрицательные относительные оценки, то повторяют с пункта3.

Этот метод используют при большом числе переменных, с помощью него можно получить экономическую интерпретацию полученного решения и провести анализ модели на чувствительность.