Задачи динамической оптимизации: Методические указания по проведению практических занятий и самостоятельной подготовки, страница 3

Образуем функцию Н

Составим уравнение Эйлера для функции (25)

Окончательно запишем

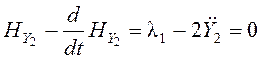
или

После первого интегрирования (27) находим закон изменения управляющего воздействия

Повторно интегрируя, найдем оптимальный процесс:

Для нахождения трех неизвестных в (29) (неопределенного множителя l₁ и постоянных интегрирования С₁ и С₂) используем уравнение для граничных условий (22) и равенство (23). Подставив в (29) t = 0 и учитывая, что Y₂(0) = 0, находим С₂ = 0. Подставляя в (29) t = Т и учитывая, что Y₂(Т) = 0, получим первое уравнение для определения l₁ и С₁:

Интегрируя (29) в пределах 0 ≤ t≤ T и учитывая равенство (23), получим второе уравнение для определения:

Решая совместно (30) и (31) относительно l₁ и С₁, находим

Учитывая (32) и (33) и С₂ = 0, можно окончательно записать уравнение для оптимальных процессов  и

Графики, соответствующие формулам (34), приведены на рис. 2. Как видно из рисунка, управляющее воздействие  (ток якоря дигателя) должен меняться по линейному закону, скорость  – по параболе.

Таблица 1 – Варианты заданий по применению уравнения Эйлера
 для нахождения оптимального управления

Варианты задания включают критерий, уравнение объекта и ограничения: 147, 148, 157, 158, 246, 248, 256, 258, 346, 347, 356, 357.

Практическое занятие 3

Принцип максимума Понтрягина и его применение для решения задач
оптимального управления

В ряде практических зада оптимизации объектов экстремум рассмотренного выше функционала при приведённых уравнениях объекта обеспечивается при управлении U(t), имеющем разрывы первого рода. Координаты объекта также могут иметь разрывы, положение которых заранее не известно. Наиболее эффективным методом решения задач такого класса является разработанный коллективом советских ученых под руководством академика Л.С. Понтрягина принцип максимума.

Для использования принципа максимума вводится скалярная функция – гамильтониан Н вида

где f₀ = G(X, U), X¢₀ = G(X, U); G(X, U) – подынтегральное выражение критерия оптимальности; f _k(X, U) – соответствует системе уравнений (2) k = 1, …, n; y_k – вспомогательная переменная, удовлетворяющая уравнению вида

Необходимые и достаточные условия оптимальности в случай линейных систем (основная теорема принципа максимума):

если правление  и соответствующая ему траектория оптимальны и удовлетворяют ограничениям (4) и (5), то можно найти не нулевую непрерывную (n + 1)-мерную вектор-функцию y_k(t) = [y₀(t), y₁(t), …, y_n(t)], которая удовлетворяет системе уравнений (36);

функция 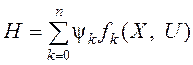 достигает максимума по переменной U и в каждый момент времени на интервале t₀ ≤ t ≤ t_k;