Назначение схемы и области применения лопаточных машин. Основные параметры, характеризующие работу ЛМ. Основное уравнение турбомашин. Уравнение Эйлера для турбомашин. Схема и принцип действия ступени осевого компрессора. Характеристика ступени осевой турбины, страница 2

 – давление рабочего тела, посчитанное по заторможенным параметрам,

 – газодинамическая функция

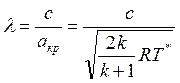
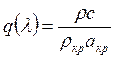<1,

  – плотность тока.

                     

	Рис. 4

Уравнение закона сохранения энергии. Тепловая форма.

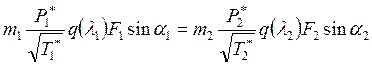
 Уравнение теплосодержания.

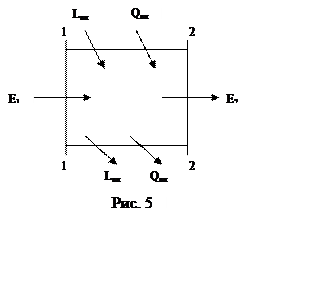
Уравнением сохранения энергии принято называть выражение закона                сохранения                энергии, записанное       применительно к             газовому потоку, протекающему через

какой–либо из элементов двигателя. Для составления этого уравнения выделим рассматриваемый элемент двумя сечениями, нормальными к направлению скорости потока (рис. 5).

Обозначим полный запас энергии газа в сечении 1–1 через Е₁, а в сечении 2–2 через Е₂. Между рассматриваемыми сечениями к газу может быть подведена (отведена) энергия из вне Е_вн.

Для принятых обозначений на основе общего закона сохранения энергии можно записать

Согласно этой записи полная энергия газового потока на выходе из рассматриваемого элемента больше (меньше) полной его энергии на входе на величину энергии, подведенной (отведенной) между рассматриваемыми сечениями.

Полная энергия 1 кг газа в каждом сечении состоит из внутренней энергии , кинетической  и потенциальной энергии давления (энергии проталкивания) . Потенциальной энергией положения пренебрегаем, т.к. . Таким образом,

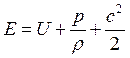
Из уравнения состояния идеального газа известно, что .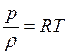

Тогда выражение для полной энергии примет вид

,

.

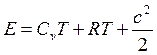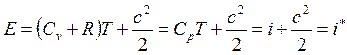Уравнение сохранения энергии преобразуется к следующему виду

или

,

.

Для энергоизолированных процессов уравнение сохранения энергии в частном случае имеет вид

Оно показывает, что при отсутствии энергообмена полная энергия газового потока в любом сечении элемента двигателя сохраняется неизменной и равна энтальпии заторможенного потока.

Рассмотрим два частных случая.

Компрессор. При условии отсутствия теплообмена через стенки корпуса , а

,

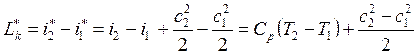где 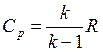 – удельная теплоемкость при постоянном давлении.

.

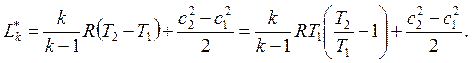
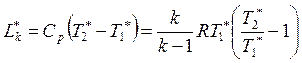Запишем уравнение политропы

,

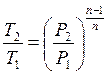тогда

,

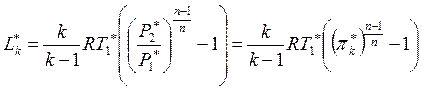где 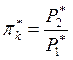 – степень сжатия в компрессоре.

Турбина. . ,

аналогично компрессору

,

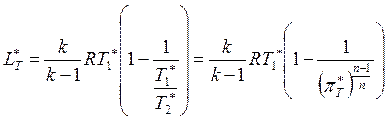где 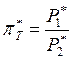 – степень расширения в турбине.

ЛЕКЦИЯ №3

Первое начало термодинамики.

Для определения параметров состояния газа при осуществлении термодинамического процесса используется уравнение первого закона термодинамики. Оно является частным выражением закона сохранения энергии для элементарного объема газа, написанным в системе координат, движущейся вместе с рассматриваемым элементом объема или, в частном случае, для покоящегося газа.

Уравнение первого закона термодинамики для элементарного объема газа имеет вид

,

т.е оно показывает, что все тепло, подведенное к рассматриваемому объему газа, идет на изменение внутренней энергии  и на совершение работы  против сил давления, связанной с изменением объема газа.

,

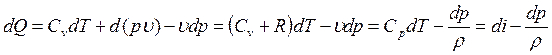Интегрируя полученное выражение, считая течение одномерным и относя все величины к 1 кг газа, получим

.

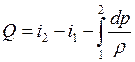В этом уравнении  – все тепло, которое подводится к газу между сечениями 1–1 и 2–2. Оно состоит из тепла , подводимого к объему газа из вне, и того тепла , которое выделяется в результате работы сил трения. Следовательно,

.

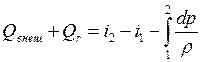Величина интеграла 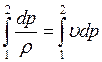 представляет собой, как известно из термодинамики работу сжатия движущегося газа. Если аппроксимировать процесс изменения состояния газа уравнением политропы 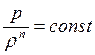 с показателем , то тогда

.

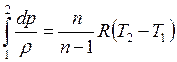Учитывая, что 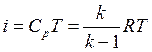, найдем

.

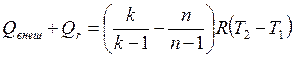 Обобщенное уравнение Бернулли. Уравнение закона сохранения энергии в механической форме.

Запишем уравнение первого закона термодинамики и вычтем из него уравнение теплосодержания для одного и того же процесса:

–

,

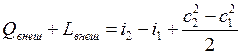
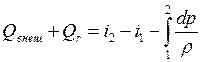получим

,

,

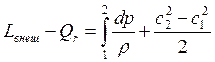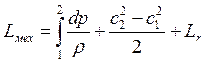где  – работа, затраченная на преодоление сил трения, которая перешла в тепло ().