Тепло,
поступающее в помещение ![]() > Q1.
> Q1.
РЕШЕНИЕ.
Рассматриваем тепловую и холодильную машину как единую термодинамическую
систему, в которую поступает тепло ![]() при температуре Т1,
тепло Q3 от окружающей среды при
температуре Т3 и выводится тепло
при температуре Т1,
тепло Q3 от окружающей среды при
температуре Т3 и выводится тепло ![]() при
температуре Т3.
при
температуре Т3.
Применим теорему Клаузиуса для приведенных теплот обратимого цикла 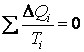 . Имеем:
. Имеем:
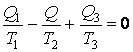 .
.
Исключая Q3 из Q = Q1 + Q3, получаем:
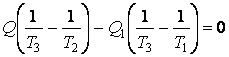 и
и
 .
.
С учетом объективных данных T1
> T2 > T3
мы видим, что в системе с динамическим отоплением Q > ![]() .
.
ЗАДАЧА
4. Определите изменение энтропии при изотермическом сжатии 1 моля кислорода от
объема V0 до объема ![]() .
.
|
ДАНО:
|
|
|
АНАЛИЗ.
При уменьшении объема газа уменьшается и число возможных микросостояний молекул
газа. В данном случае энтропия моля газа будет уменьшаться. Для расчета
изменения энтропии удобнее воспользоваться ее определением по Клаузиусу ![]() . Заметим, что при изотермическом
сжатии изменения внутренней энергии газа не происходит и в соответствии с
первым началом термодинамики теплота, поступающая в систему, идет на совершение
внешней работы.
. Заметим, что при изотермическом
сжатии изменения внутренней энергии газа не происходит и в соответствии с
первым началом термодинамики теплота, поступающая в систему, идет на совершение
внешней работы.
РЕШЕНИЕ.
![]() ;
; ![]() ;
; ![]()
 .
.
Проверка размерности:
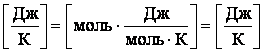 .
.
Расчет: ![]() Дж/К.
Дж/К.
ОТВЕТ: ![]() Дж/К.
Дж/К.
ЗАДАЧА 5. Показать, что для идеальных газов эффект Джоуля-Томсона не имеет места.
АНАЛИЗ.
Изменение температуры газа при его стационарном течении через пористую
перегородку называется эффектом Джоуля – Томсона. В этом конкретном случае
сохраняющейся величиной является не внутренняя энергия U,
а энтальпия ![]() . Энтальпия – термодинамическая
функция состояния, в которой в качестве независимых переменных берутся энтропия
S и давление p:
. Энтальпия – термодинамическая
функция состояния, в которой в качестве независимых переменных берутся энтропия
S и давление p: ![]() . Запишем дифференциал H применительно к рассматриваемому эффекту:
. Запишем дифференциал H применительно к рассматриваемому эффекту:
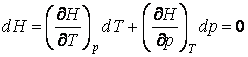 .
(1)
.
(1)
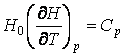 , следует уточнить значение
, следует уточнить значение 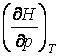 .
.
Из определения энтальпии ![]() следует
следует ![]() .
.
Откуда получаем 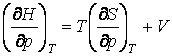 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.