Получение соотношений для определения кинематических параметров судна

4 марта 2005 г.

ПОЛУЧЕНИЕ СООТНОШЕНИЙ  ДЛЯ ОПРЕДЕЛЕНИЯ

КИНЕМАТИЧЕСКИХ ПАРАМЕТРОВ СУДНА

Полагаем,  что линия,  являющаяся осью  вспомогательной координатной

системы,  лежить на пересечении плоскостей

                           и        

Следовательно,  ее  уравнение

                                                   (1)

где  (Линия в плоскости, параллельной плоскости , может рассматриваться как результат ее пересечения плоскостью, у которой   при )

Полагаем,  что эта линия, являющая осью  вспомогательной координатной системы, перпендикулярна  к   оси КПА,  уравнение которой

представим в виде

                            

Ось  КПА полагаем осью   вспомогательной координатной системы.

Ее направляющие косинусы  равны направляющим косинусам НУП КПА

i - й  антенны

                                 

То есть 

Из условия ортогональности осей      и 

 получаем: 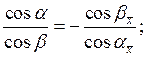   т. е.   и 

Выражения для направляющих косинусов третьей оси -  вспомогательной координатной системы получим также из условий ее ортогональности осям      и  ,  которые приведем в виде

                                           

                                           

Решая данную систему уравнений  относительно ,  получим

     

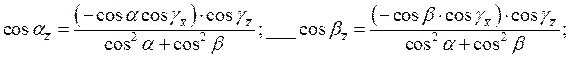
Учитывая также,  что,  получим

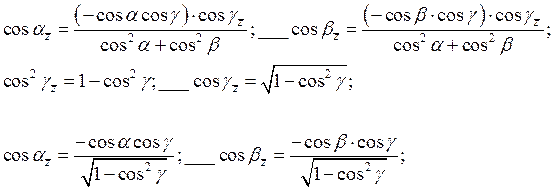
или  

При КПА  на угол   при  ее начальном угловом положении   угловое положение антенны в й  момент  времени , а ее координаты

будут  равны

       

Тогда,  учитывая,  что  (см. с.80 Г.Корн) направляющие косинусы осей ,,  равны соответственно  

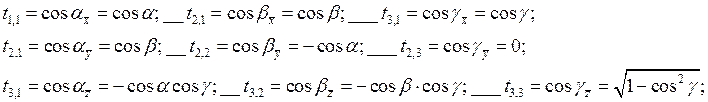
координаты КПА в координатной системе  получим в виде:

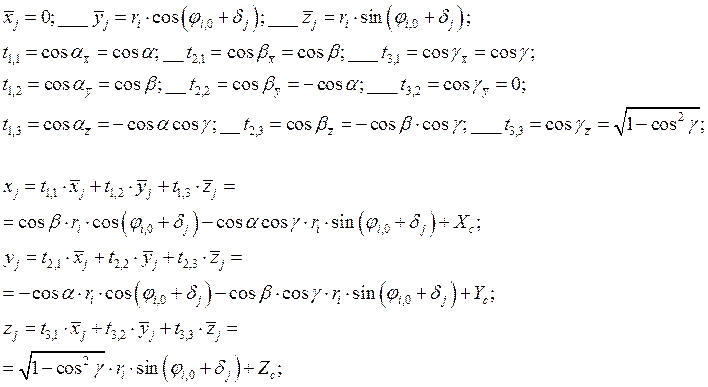
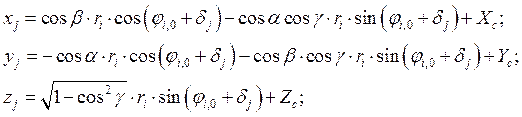
направляющие косинусы оси    будут 

Выбираем в плоскости КПА точку  с координатами    и 

            Координаты точки   из уравнения НУП получим в виде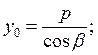  

Составим уравнение прямой линии, проходящей через точки    и    - центр  КПА

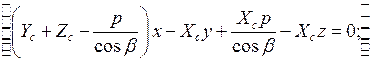                                           ( 2 )

,  производя в соответствии с §154 (с.185 Выг.) преобразования

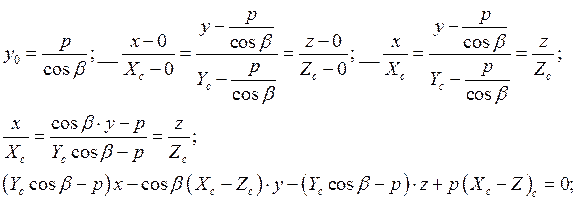
Определим  направляющие косинусы этой линии, которую полагаем осью 

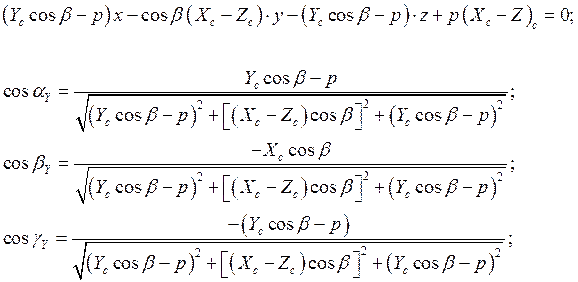
Направляющие косинусы  оси    определим,  учитывая, что  линия  нормальна осям     и  .  Следовательно, верны соотношения

                                

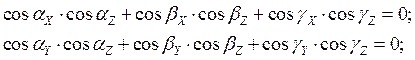
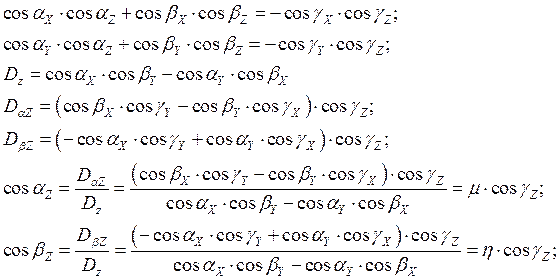
Используя также третье соотношение    определяем вели чины направляющих косинусов и  оси  .

Определим положение точки А_i   в  координатной системе, центр  O_c  которой с координатами X_c, Y_c,  Z_c  (в выбранной горизонтной системе координат) расположен на оси кругового перемещения антенн.  Ось  O_c X_c     находится в плоскости кругового перемещения антенн,  нормальна к  оси вращения и параллельна плоскости   XOY   горизонтной системы.   Ось  O_c Y_c , также   находящаяся в плоскости кругового перемещения антенн,  нормальна к  оси вращения и  оси  O_c X_c  .   Угол поворота δ _i   отсчитываем относительно оси    O_c Y_c   .   Тогда   координаты точки   в координатной системе   X_c O_c Y_c   

                                               

Расстояние    от проекции  оси  O_c X_c       на плоскость  XOY    при этом   будет равно    

Расстояние    от  центра  O_c    вдоль  оси  O_c X_c       (на плоскости  XOY )   при этом   будет равно   центр  O_c