Исследовалась
зависимость числа(y) изготовляемых деталей в час от числа работающих
токарных станков различной производительности ![]() . Независимое переменное принимало
значения 10, 20, 30, 40, 50. Основной уровень
. Независимое переменное принимало
значения 10, 20, 30, 40, 50. Основной уровень ![]() равен 30, интервал варьирования I равен 20. Кодирование значения равны:
-1; -0,5; 0; 0,5; 1.
равен 30, интервал варьирования I равен 20. Кодирование значения равны:
-1; -0,5; 0; 0,5; 1.
Исходные данные можно теперь представить в виде табл. 1, матрицы независимых переменных.
Таблица 1
Матрица независимых переменных
|
Номер опыта |
x0 |
x1 |
|
Первый |
1 |
-1 |
|
Второй |
1 |
-0,5 |
|
Третий |
1 |
0 |
|
Четвертый |
1 |
0,5 |
|
Пятый |
1 |
1 |
В матрице имеются
два вектор-столбца: вектор-столбец "фиктивной" переменной х0
и вектор-столбец переменной х1, а также пять вектор-строк. Введение
вектор-столбца х0 дает возможность от двух формул для расчета
коэффициентов регрессии: 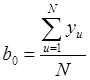 ,
, 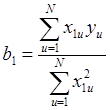 , перейти к одной:
, перейти к одной:
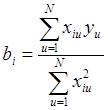 , i = 0,1.
, i = 0,1.
Для расчета коэффициентов регрессии к матрице независимых переменных добавляют вектор-столбец результатов опытов (табл. 2).
Таблица 2
Матрица независимых переменных и результатов опытов
|
Номер опыта |
х0 |
х1 |
у |
|
Первый |
1 |
-1 |
92 |
|
Второй |
1 |
-0,5 |
118 |
|
Третий |
1 |
0 |
148 |
|
Четвертый |
1 |
0,5 |
182 |
|
Пятый |
1 |
1 |
210 |
Коэффициенты регрессии равны:
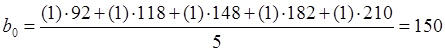 ,
,
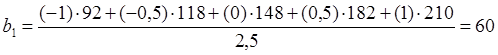 .
.
Уравнение регрессии: у 150 + 60х1.
В приведенной матрице выполняется условие
ортогональности вектор-столбцов: 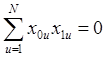 . Коэффициенты регрессии определяются независимо
друг от друга.
. Коэффициенты регрессии определяются независимо
друг от друга.
После расчета коэффициентов регрессии производится статистический анализ уравнения, называемый проверкой адекватности модели.
Проверка адекватности включает следующие операции:
1. Расчет дисперсии воспроизводимости. Рассмотрим случай, когда в каждом опыте было проделано равное число n параллельных наблюдений. Дисперсия среднего арифметического каждого опыта:
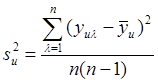 ,
, 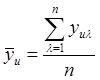 .
.
Далее с помощью критерия Кохрена проверяется гипотеза об однородности дисперсии. Величина критерия Кохрена равна отношению максимальной дисперсии к сумме всех дисперсий:
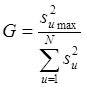 .
.
Значения G-критерия для уровней значимости 0,05 и 0,01 приведены в табл. 4 Приложения, где f = n-1. Если рассчитанное значение критерия окажется меньше табличного, то гипотеза об однородности дисперсий принимается. Однородность дисперсий позволяет рассчитать оценку дисперсии воспроизводимости всего эксперимента:
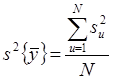 .
.
Число степеней свободы этой оценки равно N(n-1).
2. Расчет суммы квадратов для проверки гипотезы адекватности:
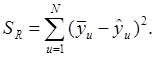
3. Расчет дисперсии для проверки гипотезы адекватности ![]() :
:
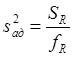 ,
,
где fR = N - m, m - число определяемых коэффициентов регрессии. Для линейного случая и одного фактора m = 2.
4. Расчет критерия Фишера F и проверка гипотезы адекватности:
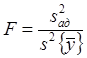 .
.
Рассчитанное значение критерия Фишера сравнивается с табличным значением обычно для уровня значимости 0,05 (Приложение, табл.1) и степеней свободы: fR для числителя и N(n-1) для знаменателя.
Кроме того, при статистическом анализе (перед проверкой адекватности) проверяется гипотеза о значимости коэффициентов регрессии. Для этого удобно пользоваться t-критерием. В первую очередь необходимо рассчитать дисперсии коэффициентов регрессии:
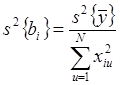 i = 0,1.
i = 0,1.
Затем вычисляется t-критерий:
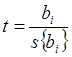 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.