Отказы как случайные величины, их основные характеристики. Теоретические законы распределения случайных величин. Закон нормального распределения и его свойства

Лекция № 5.  Вероятностные оценки отказов  (2 часа)

Учебные вопросы:

1.  Отказы как случайные величины, их основные характеристики (функциональные - функция и плотность распределения; числовые – математическое ожидание, дисперсия, среднеквадратичное отклонение, коэффициент вариации, квантиль, медиана, мода).

Лекция № 6.  Продолжение лекции № 5  (2 часа)

Учебные вопросы:

2.  Теоретические законы распределения случайных величин.

3.  Закон нормального распределения и его свойства.

1.  Отказы как случайные величины, их основные характеристики

Отказ – событие, заключающееся в полной или частичной потере работоспособности. По причинам возникновения отказы могут быть случайные и систематические.

Случайные отказы – из-за непредусмотренных перегрузок, дефектов материала, погрешностей изготовления и т.д.

Систематические отказы– вследствие закономерных явлений, вызывающих постепенное накопление повреждений или изменение характеристик (влияние окружающей среды, нагрузки, времени, etc., вследствие чего развивается коррозия, происходит износ, усталость, ползучесть, старение изоляции, etc.).

Процесс разработки, сооружения и эксплуатации мостовых сооружений определяют многочисленные факторы, точный учет которых по самым различным причинам невозможен. Эти факторы носят случайный характер, но влияют на их надежность и работу. Поэтому наше внимание должно быть уделено не только систематическим, но и случайным отказам. То есть отказ надо рассматривать как случайную величину.

Для того, чтобы ознакомиться с основными зависимостями теории надежности, необходимо кратко напомнить ранее изученный в других дисциплинах материал.

Пусть Х – случайная величина, а {Х} – диапазон ее изменения. Для реальных объектов {Х} всегда ограничен (например, прочность материала может быть очень маленькой, если в образце имеется скрытый дефект, или очень большой, но всё-таки не бесконечной). Часто для удобства математических действий диапазон {Х} принимают неограниченным. В большинстве случаев это не сказывается на конечных численных результатах, но создает значительные математические удобства.

Случайные величины описываются двумя функциональными и несколькими числовыми характеристиками.

Функциональные характеристики случайной величины

Функция распределения случайной величины

Пусть х – некоторое фиксированное значение случайной величины Х из диапазона ее изменения {Х}.

Для любого множества случайных чисел {Х} всегда имеется некоторая вероятность Р того,  что  случайная величина Х не будет больше этого значения  х, т. е.  Р (Х < х).   Эта вероятность обозначается

F(x) = Р (Х<х)

и называется функцией распределения или функцией вероятности случайной величины Х.

Функция F(x) является неубывающей функций, возрастающей от 0 до 1 в пределах изменения {Х} случайной величины Х монотонно (для непрерывных процессов) или ступенчато (для дискретных процессов)

F(x)
1,0
0	Х

Непрерывные процессы: значения прочности образцов (прочность может принять любое значение).

Дискретные процессы: количество разрушенных образцов при заданной нагрузке.

Плотность распределения случайной величины

Плотность распределения f(x) является производной от функции распределения F(x) по текущей переменной х:

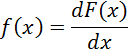
Следовательно

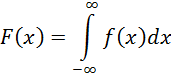
F(x)
1,0
F(x)
0		х					Х

f(x)
	f (x) F(x)
0		х		Х

Числовые характеристики случайной величины

Математическое ожидание (среднее значение)

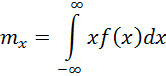
- для непрерывной величины,

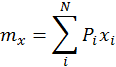
- для дискретной случайной величины,

где Р_i  –  вероятность появления  х_i;

х_i–  i-тое  значение случайной величины;

N  –  общее число наблюдений;

i –  число наблюдений (опытов). 

Значение математического ожидания, определяемое по результатам наблюдений как для непрерывной, так и для дискретной случайной величины, называется оценкой математического ожидания  х  или средним значением:

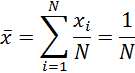
Дисперсия случайной величины

Дисперсия («рассеяние») случайной величины – это математическое ожидание квадрата отклонения этой случайной величины от её математического ожидания

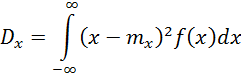
- для непрерывной величины,

а для дискретной случайной величины

.

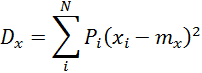
Оценка дисперсии случайной величины по результатам наблюдений:

 

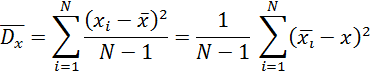
                   Среднеквадратичное отклонение

s_x= Ö D_x  .

Коэффициент вариации

v_x  = s_x / m_x .

Квантúль – значение случайной величины, соответствующее заданной вероятности.

Медиана – это квантиль, соответствующий вероятности 0,5. Площадь на графике функции f(x) делится медианой пополам.

Мода – наиболее вероятное значение случайной величины. При этом на графике функции F(х) - точка перегиба, а у функции f(x) – максимальное значение.

Для симметричного распределения медиана, мода и математическое ожидание совпадают.

2.  Теоретические законы распределения случайных величин

Конкретный вид функции распределения случайных величин зависит от конкретно решаемой задачи. По результатам экспериментов и наблюдений могут быть построены