

Пример 2.6 (стр. 38) из книги Яблонского Ф. М.
Произвести интерполяцию промежуточных точек прямой, заданной координатами (Xн=3, Yн=2, Xк=14, Yк=7)
1. В соответствии с алгоритмом отмечаем начальную точку с координатами Xн; Yн (рис. 2.12).
2. Определяем (Xк-Xн)=10 и (Yк-Yн)=4
3. Даем единичное приращение по координате X1=2+1=3 и производим суммирование значения 10/2+4=9, сравнивая полученные значения (Xк-Xн)=10. Так как условие (2.34) не выполняется, то ∆Y1=0. Отмечаем точку с координатами X1=3; Y1=1 (R=9).
4. Даем приращение по координате X: X2=3+1=4, производим суммирование предыдущего результата со значением (Yк-Yн)=4, поучаем в результате 13, условие (2.34) выполняется. Следовательно, ∆Y2=1. Отмечаем точку с координатами X2=4; Y2=2. Вычитаем из полученной суммы 10, получаем остаток R=3.
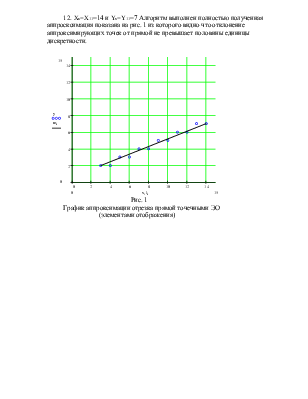
5. продолжаем операции в соответствии с алгоритмом до значения X=Xк=12. Полученная аппроксимация показана на рис.2.12, из которого видно, что отклонение аппроксимирущих точек от прямой не превышает половины единицы дискретности.
Следует
отметить, что формулы (2.30) – (2.34) и блок-схема алгоритма справедливы только
для условия, когда │Yк-Yн│≤│Xк-Xн│. При нарушении этого условия выражение (2.32)
следует заменить на 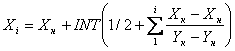 . (2.35)
. (2.35)
Следовательно, блок-схему алгоритма рис.2.11 надо дополнить операцией поверки условия sign(│YR-Yн│-│Xк-Xн│), в зависимости от выполнения которого осуществляется выбор уравнения (2.32) или (2.35) (sign обозначает знак результата в круглых скобках). Кроме того, необходимо также проверить значение функции sign(Xк-Xн) и sign(Yк-Yн), которые определяют направления приращения координат X и Y. При положительном значении указанных функций адресные счетчики работают в режиме суммирования, а при отрицательном знаке – в режиме вычитания.
Задание:
Произвести интерполяцию промежуточных точек прямой, заданной координатами (Xн=3, Yн=2, Xк=14, Yк=7)
1. В соответствии с алгоритмом отмечаем начальную точку с координатами Xн; Yн (рис. 1)
Определяем (Xк-Xн)=11 и (Yк-Yн)=5
Даем единичное приращение по координате X1=3+1=4 и производим суммирование значения 11/2+5=9.5, учитывая что формула 2.32 определяет целочисленные значения получаем R=10 сравнивая полученные значения
c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y1=0. Отмечаем точку с координатами X1=4; Y1=2 (R=10).
2. Даем приращение по координате X: X2=4+1=5, производим
суммирование предыдущего результата R=10 со значением (Yк-Yн)=5, получаем в результате 15, условие (2.34) выполняется. Следовательно, ∆Y2=1. Отмечаем точку с координатами X2=5; Y2=3. Вычитаем из полученной суммы 11, получаем остаток R=4.
3. Даем единичное приращение по координате X3=5+1=6 и производим суммирование значения R=R+(Yк-Yн)=4+5=9 и сравниваем c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y3=0. Отмечаем точку с координатами X3=6; Y3=3 (R=9).
4. Даем приращение по координате X: X4=6+1=7, производим суммирование предыдущего результата R=9 со значением (Yк-Yн)=5, получаем в результате 14, условие (2.34) выполняется. Следовательно, ∆Y4=1. Отмечаем точку с координатами X4=7; Y4=4. Вычитаем из полученной суммы 11, получаем остаток R=3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.