Сигналы и их характеристики. Линейные инвариантные к сдвигу цепи

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №1

по курсу «Теория Электрической Связи»

РГЗ – 1

Вариант 8. Подвариант 2.

Выполнил:

Студент 2 курса

Группы РТС9-82

Факультета РЭФ

Полукеев О.В.

Проверил:

Тонконогов Е.А.

Новосибирск

2010

Контрольное задание №1

1.Сигналы и их характеристики

Дан сигнал, он определяется восьмизначным равномерным кодом согласно варианту и подварианту, где символ «0» соответствует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 1 мкс.

Сигнал: 00100110

Запишем математическую модель сигнала в виде линейной комбинации функций Хевисайда и построим временной график

·                 Найдем спектр сигнала в базисе Уолша и построим спектральную диаграмму

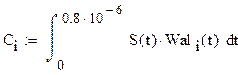
Для этого воспользуемся данной формулой: Wal_i(t) - функция Уолша i-ого порядка. i изменяется от 0 до 8.

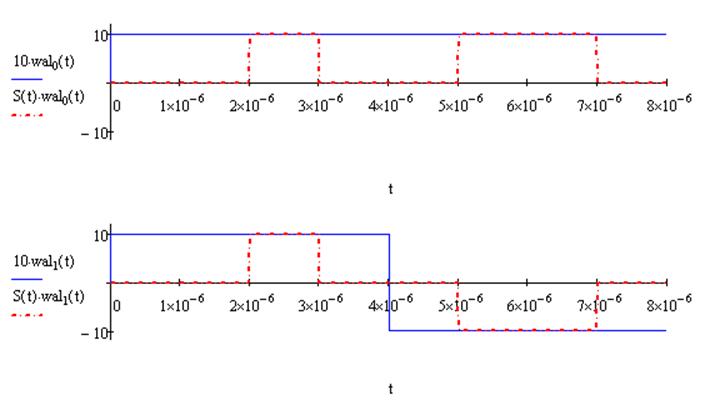
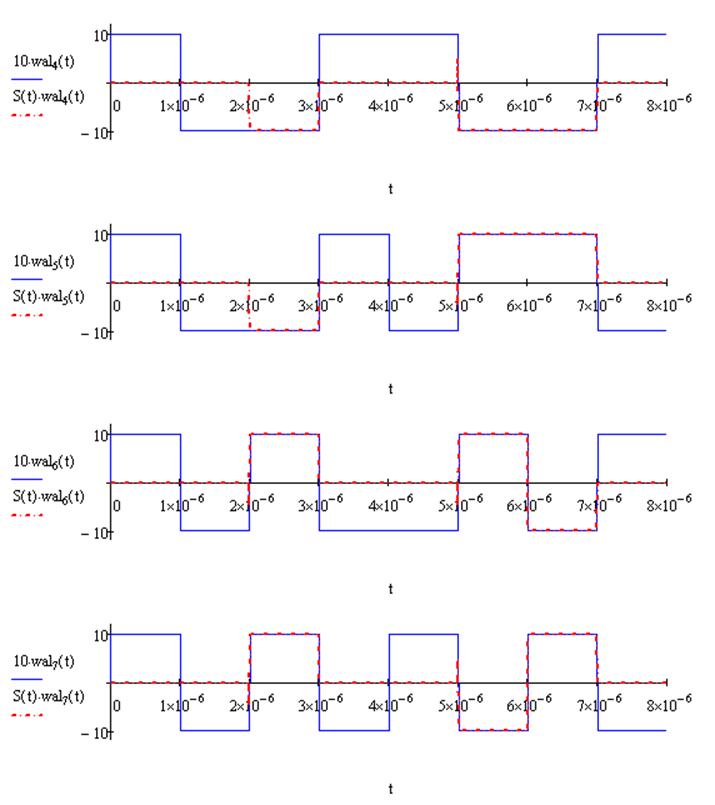
Спектр сигнала в базисе Уолша будет иметь вид:

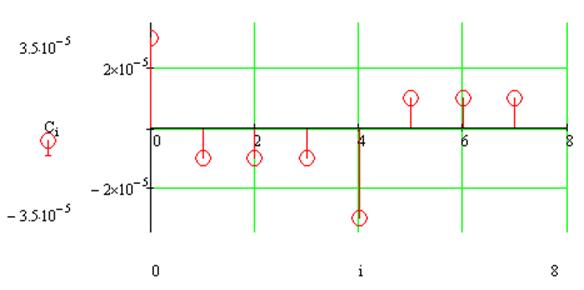
·  Найдем аналитически спектральную плотность прямоугольного видеоимпульса относительно ядра Фурье

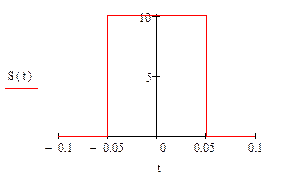
За прямоугольный видеоимпульс примем:               

Время t – мкс

Напряжение S(t) – B.

Значение спектральной плотности прямоугольного импульса находится из формулы:

Используем, одну из основных теорем о спектрах: теорему о спектре сигнала смещённого во времени на :

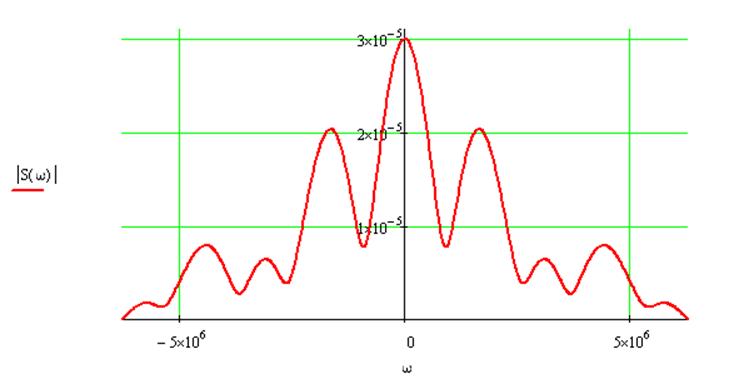
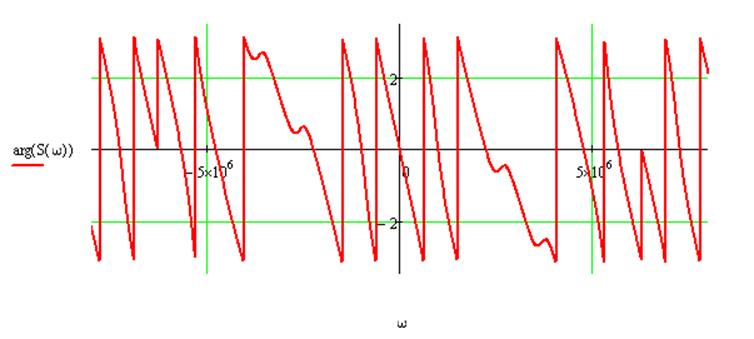
·  Пользуясь свойствами преобразования Фурье, найдем спектральную плотность заданного сигнала относительно ядра Фурье, построим графики её модуля и аргумента.

Наш сигнал имеет вид:

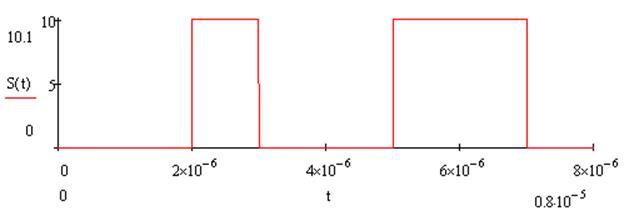
Используют прямое преобразование Фурье и теорему сдвига для нашего сигнала:

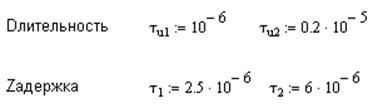
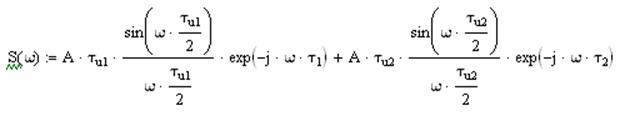
Где S(ω) - спектральная плотность (в комплексной форме).

Откуда графики модуля и аргумента выглядят следующим образом:

 

·  Найдем спектр периодической последовательности, полученной повторением данного сигнала, относительно комплексного базиса Фурье, и построим амплитудную и фазовую спектральные диаграммы

Формула для спектра периодической последовательности, полученной повторением данного сигнала относительно базиса Фурье, имеет вид:

 

Где T=8 мкс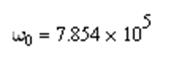              

Для наглядности графики спектральных диаграмм изобразим совместно:

 

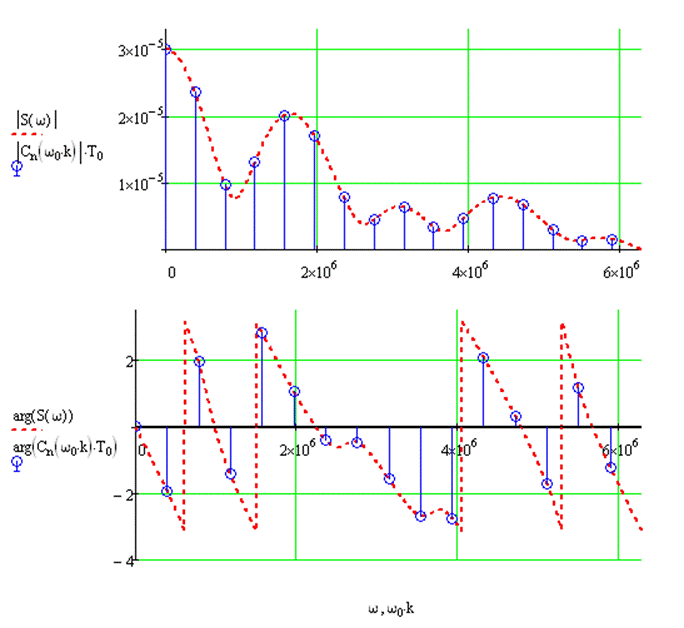·  Найдем автокорреляционную функцию сигнала и  построим ее график.

Формула для автокорреляционной функции имеет вид:

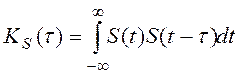
Здесь с – задержка сигнала

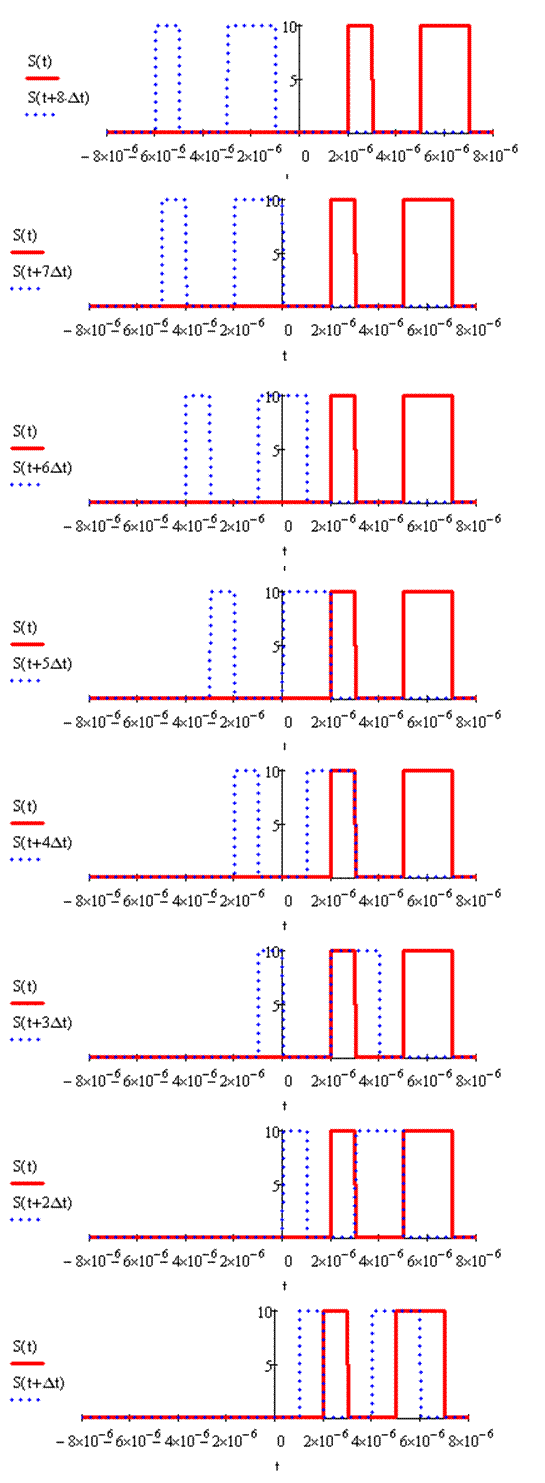
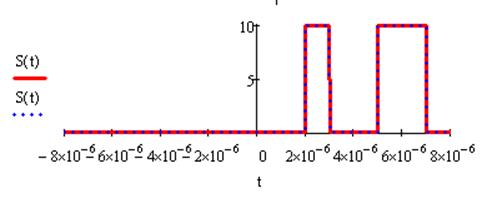
Рассмотрим графически произведение S(t)∙S(t - τ)

 

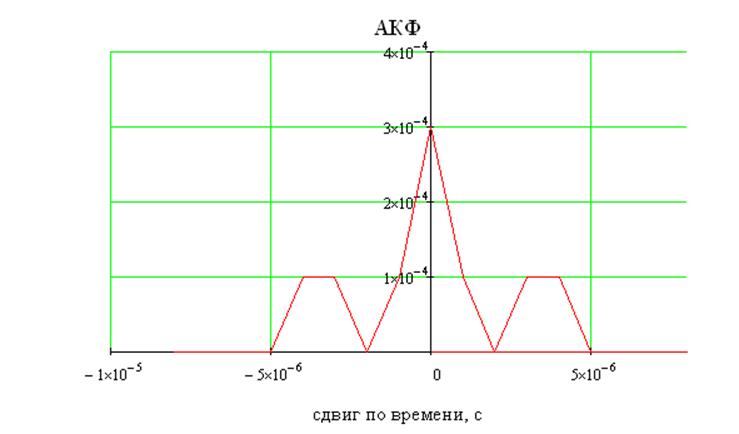
Для правильного определения автокорреляционной функции, рассмотрим ее своиства:

1.  При автокорреляционная функция достигает максимума.

S(0)=max

2.  Автокорреляционная функция обладает свойством сопряженной симметрии

S(τ)=S(-τ)

 

·  Определим эффективную ширину спектра

Полная энергия одиночного импульса может быть вычислена либо во временной области, либо в частотной в соответствии с равенством Парсеваля:

 

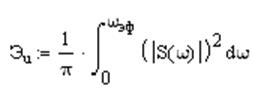     В частотной области можно определить эффективную ширину спектра сигнала. Это такой частотный интервал, в котором сосредоточена подавляющая часть полной энергии сигнала. Обычно 90% или 95%.

   Найдём эффективную частоту . Для этого изобразим график функции:

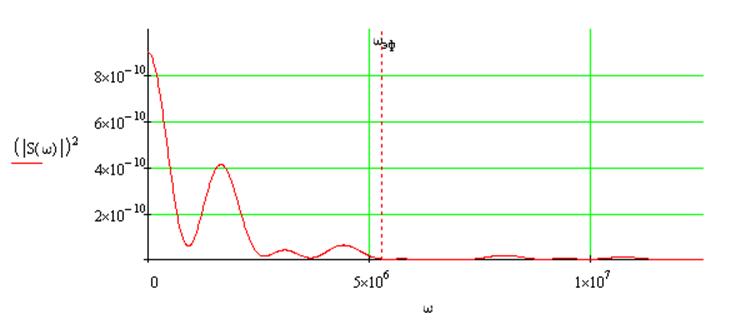
   Глядя на график видно, что основная энергия сигнала сосредоточена в частотном интервале приблизительно равном: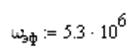

   Подставляя в данный интеграл , находим, что эффективная ширина спектраLполовина энергии)

 

В данном случае мы предполагали лишь положительную область спектра, но в силу симметричности для всей области спектра эффективная ширина его умножается на 2.

 

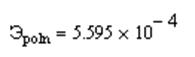·  Найдем сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ и построим временной график полученного сигнала.

Частота среза фильтра f_ср=2.7 МГц, а крутизна ФЧХ S’=0.8 рад/МГц.

Определим передаточную функцию цепи имея данные значения частоты среза  фильтра и крутизны :

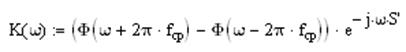
где  вышеупомянутая функция Хевисайда

 

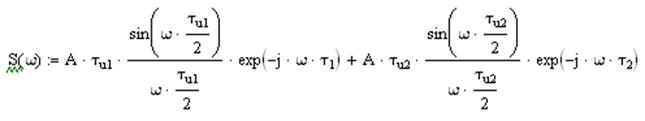Выходной сигнал в частотной области имеет вид:

Используя обратное преобразование Фурье, определим выходной сигнал:

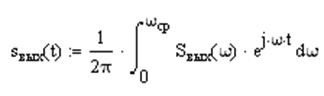
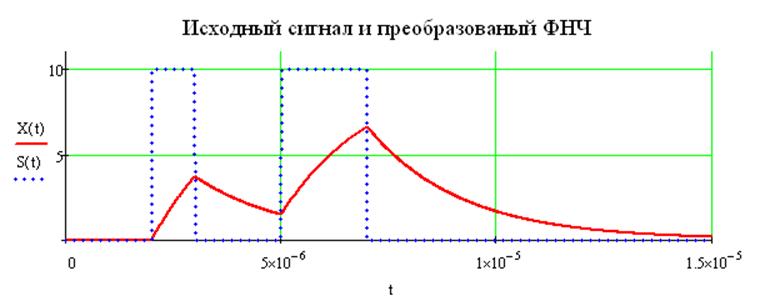
Построим график полученного выходного сигнала:

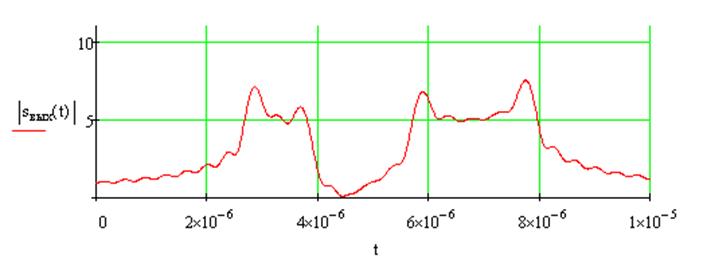
·  Найдем сигнал, который получается из заданного при воздействии RC-фильтра НЧ и построим временной график полученного сигнала

R=2.7 кОм

С=0.8 нФ

Из заданных параметров определим постоянную времени:

τ =R∙C=2.16 мкс

Для определения выходного сигнала воспользуемся импульсной характеристикой:

Подставив ее в следующую формулу, получим сигнал на выходе:

 

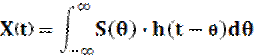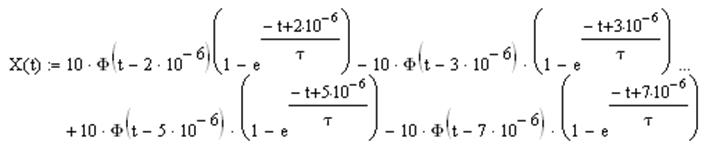
Построим ее график:

Линейные инвариантные к сдвигу цепи.

2.1  ЛИС-цепь определяется схемой согласно варианту (табл. 4), её параметры (R в кОм, С в мкФ, L в мГн) – согласно подварианту (табл. 5).

Таблица 4.Таблица 5.

Подвариант	5
R1	2.3
R2	1.5
C1	0.5
C2	0.5
L1	1.9
L2	1.0

8

2.2     Требуется:

●  Найти комплексную частотную характеристику цепи, посторить графики АЧХ и ФЧХ.

Решение: Запишем исходный сигнал, используя прямое преобразование Лапласа:

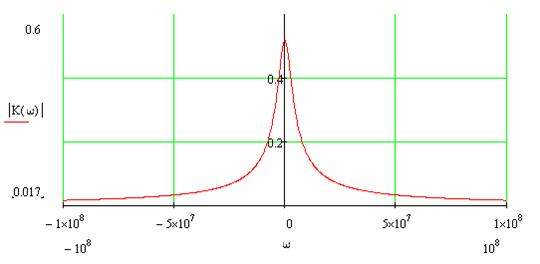заменяя на получаем:

●   Найти импульсную и переходную характеристики, построить графики:

●   Найти отклик цепи на заданный сигнал, построить