![]()
Полученную функцию ξ (t) можно выразить графически (рис. 6. 2).
Пример 6.2. В последнем примере 6.1 заменим одно из инерционных звеньев на интегрирующее:
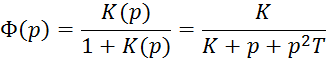
Сигнал управления возьмем тот же:
Х(t) = At
Решение. Передаточная функция замкнутой системы
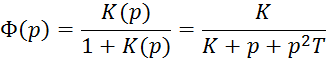
Отсюда дифференциальное уравнение замкнутой системы
![]() (6.5)
(6.5)
Будем искать ожидаемое решение, как и в предыдущем примере:
y(t)=С0+С1t
Производные функции y(t):
![]() ;
; ![]()
Подставляем y(t), ее производные и x (t) в уравнение (6.5):
С1 + КС0 + КС1t = КАt(6.6)
Приравнивая члены, содержащие t в первой степени:
KC1t = KAt,
откуда
С1 = А
Приравниваем члены, не содержащие переменную t:
С1=-KC0
откуда
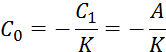
Подставляя С0 и С1, в (6. 5), получаем:
ξ(t)=x(t)–y(t)=![]()
Ошибка регулирования
ξ(t)=![]() const.
const.
Выразим графически эту зависимость (рис. 6.3)


Рис. 6. 2 Рис. 6. 3
Сравнивая рис. 6.2 и рис. 6.3, можно легко заметить, что при переходе от статической системы к астатической ошибка регулирования уменьшается при одном и том же входном воздействии x(t). В частности, если в статической системе ошибка возрастает со временем, то в астатической она постоянна и обратно пропорциональна коэффициенту усиления системы, т. е. при желании может быть снижена до необходимой величины путём повышения коэффициента усиления К.
Рассмотренный способ нахождения ошибки регулирования можно применять в ограниченных случаях, когда система имеет несложную структуру (невысокий порядок дифференциального уравнения) и при входных сигналах простой аналитической записи, когда можно более или менее удачно записать в общем виде ожидаемое решение. В иных, более сложных, ситуациях решение может быть весьма громоздким и трудоёмким, а иногда и практически невозможным.
6.2.2. Классический операторный метод определения ошибки регулирования
Как принято в операторном методе, задача решается в области Лапласовых изображений. Для определения изображения по Лапласу функции в любой точке системы берётся изображение известной функции (в данном случае – на входе системы) и умножается на передаточную функцию между входом и интересующей точкой системы. При отыскании ошибки регулирования такой точкой является выход сумматора, а такой передаточной функцией будет передаточная функция ошибки от регулирующего воздействия Кξ x(p). Ее очень просто записать, зная передаточную функцию разомкнутой системы К(р) или замкнутой системы Ф(р).
Уравнение сумматора (см. рис. 6.1) в области изображений:
ξ(р) = x(p) – y(p) (6.7)
С другой стороны,
Y(p) = X(p) Ф(р) = X(р)![]() (6.8)
(6.8)
Подставляя (6.8) в (6.7) и разделяя переменные X(р) и ξ(р), получаем их отношение, являющееся искомой передаточной функцией ошибки:
![]() (6.9)
(6.9)
или в другой форме записи:
![]() (6.10)
(6.10)
Формула (6.10) справедлива для конфигурации рис. 6.1, где изображена следящая система, в которой выход системы совпадает с инверсным входом сумматора. Для систем иной конфигурации, где в канале обратной связи может быть звено или группа звеньев, справедлива формула (6.9). Кстати, она справедлива и для следящих систем тоже, т.е. более универсальна. Таким образом, классический операторный метод отыскания ошибки сводится к четырем операциям:
1. По известной функции х(t) находят ее изображение по Лапласу.
2. По известной структуре системы К(р) находят Кξx(p) по формуле
(6. 9).
3. Перемножают: x(р)Kξx(р)=ξ(р).
4. Обратным преобразованием Лапласа с помощью специальных таблиц, имеющихся в справочниках, определяется ξ (t). Недостатком такого метода определения ошибки является высокая трудоемкость практической работы при громоздкой структуре системы или сложных аналитических записях функции х(t).
6. 3. Метод коэффициентов ошибки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.