Составление уравнений типовых процессов механообработки. Ортогональное точение деталей типа «вал» (задача с двумя степенями свободы). Устойчивость линейных непрерывных САР. Поведение свободной (переходной) составляющей при попарно сопряженных комплексных, чисто мнимых и нулевых корнях характеристического уравнения, страница 4

Первое предельное равенство соответствует устойчивой системе, а второе - неустойчивой. Если переходной процесс с течением времени не затухает и не расходится, то система находится на границе устойчивости.

Последние два режима являются неработоспособными, т.к. не отвечают целям управления объектом, заключающихся в придании ему некоторого желаемого состояния.

Применительно к переходным характеристикам устойчивость выражается предельным требованием:

 

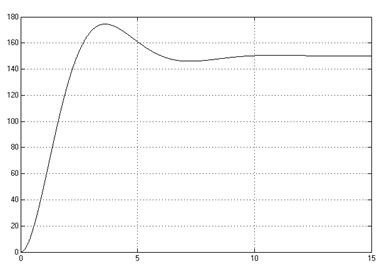
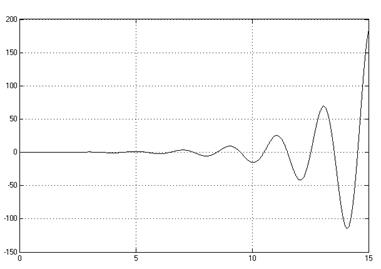
Для нелинейных систем, вводят понятия устойчивости «в малом», «в большом» и «в целом»:

•  система устойчива «в малом», если лишь констатируется факт наличия области устойчивости, но границы ее не определены;

•   система устойчива «в большом», когда определены границы области устойчивости, т.е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние;

•  система, которая возвращается в исходное состояние при любых начальных отклонениях, называется устойчивой «в целом».

Для некоторого класса систем устойчивость «в целом» называется абсолютной устойчивостью.

Все случаи исследовательской устойчивости принято подразделять на некритические и критические (по А.М. Ляпунову).

К некритическим относятся все случаи, когда вопрос об устойчивости однозначно решается на основании исследований уравнений 1-го приближения.

Применительно к САР следует рассматривать линеаризованную математическую модель по характеру собственно свободного движения, которое определяется  характеристическим уравнением D(р) = 0.

Критические случаи имеют место, когда среди корней D(р) = 0 имеются корни с нулевой вещественной частью. Тогда вопрос об устойчивости необходимо решать исследованием полного нелинейного дифференциального уравнения.

Теоремы А.М. Ляпунова.

Теорема 1. Если вещественные части всех корней характеристического уравнения 1-го приближения отрицательные, то собственное движение асимптотически устойчиво независимо от членов разложения выше 1-го порядка малости

Теорема 2. Если среди корней характеристического уравнения 1-го приближения найдется по меньшей мере один с положительной вещественной частью, то собственное движение неустойчиво независимо от членов разложения выше 1-го порядка малости.

Устойчивость линейной системы определяется ее параметрами и не зависит от внешних воздействий.

Процессы в САР описываются неоднородным дифференциальным уравнением вида:

 

Общее решение данного уравнения состоит из двух составляющих:

Здесь y_уст(t) – частное решение неоднородного дифференциального уравнения, определяемое приложенным к системе внешним воздействием;  y_уст(t) - вынужденная составляющая;

y_пер(t) – общее решение соответствующего однородному дифференциальному уравнению характеристического уравнению вида:

Поскольку только y_пер(t) описывает поведение САР после устранения внешнего воздействия, эту составляющую называют свободной (переходной) составляющей.

Корни характеристического уравнения D(p) = 0:

 с постоянными коэффициентами могут быть:

1. вещественными и различными;
2. попарно сопряженными комплексными;
3. чисто мнимыми;
4. нулевыми.

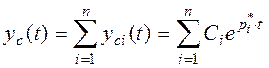В общем случае свободная составляющая выходной переменной определяется выражением:

 

где C_i  – постоянная интегрирования, зависящая от начальных условий;        – корень характеристического уравнения.

1. Корни вещественные и различные

1.1. Корни отрицательные вещественные:

С течением времени экспонента будет затухать с интенсивностью, определяемой величиной      ,

а свободная составляющая будет асимптотически стремиться к нулю                  ,  т.е. линейная непрерывная САУ является устойчивой.

1.2. Корни положительные вещественные:                ,                        .