Задание на расчетно-графическую работу
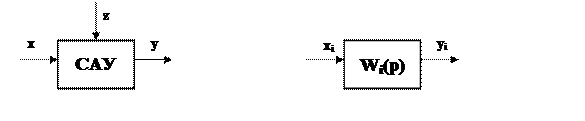 Задана система
автоматического управления (рис.1), состоящая из 4-х элементов (рис.2, i =1,2,3,4,),
Задана система
автоматического управления (рис.1), состоящая из 4-х элементов (рис.2, i =1,2,3,4,),
|
|
где приняты следующие обозначения: х – задающее воздействие; у – управляемая величина; z- возмущающее воздействие; xi – входное воздействие i-гo элемента; yi – выходная величина i-ro элемента.
Элемент i=l является объектом управления. Остальные элементы (Относятся к управляющей (усилительно-преобразующей) части САУ.
Динамические свойства элементов в общем случае описываются дифференциальными уравнениями:
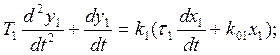 (1)
(1)
 (2)
(2)
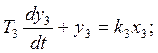 (3)
(3)
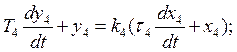 (4)
(4)
где ki, Ti, ti – параметры элементов.
Таблица 1
|
Уравнения связей |
||||
|
9 |
x3=x - y |
х4 = у3 – у4 |
x2 = y4 |
x1= y2 - z |
Примечание: у = у1
Таблица 2
|
k1 |
τ1 |
T1 |
k01 |
k2 |
τ2 |
T2 |
k02 |
k3 |
T3 |
k4 |
τ4 |
T4 |
|
|
1 |
1,0 |
1,0 |
0,8 |
0.0 |
0.5 |
1,0 |
0.2 |
0.0 |
0.5 |
0.0 |
0.5 |
0.4 |
0.3 |
Требования к качеству скорректированной САУ:
1. Статические (установившиеся)
ошибки при отработке единичных ступенчатых
воздействий (задающего и возмущающего) не должны превышать 5% от заданного
значения управляемой величины. Если система астатическая, то необходимо
обеспечить
5%-ую ошибку при отработке линейно изменяющегося задающего воздействия (для
упрощения можно считать скорость его изменения равной единице).
2. Длительность переходного процесса должна быть обеспечена на порядок меньше, чем в исходной системе.
3.Перерегулирование при отработке единичного ступенчатого задающего воздействия не должно превышать 5% от установившегося значения управляемой величины.
Глава 1. Анализ исходной системы.
1.1. Построим структурную схему в порядке нумерации элементов, размещая их справа налево
Конкретизируем выражения уравнений, подставив в них значения равные единице и нулю.
 (5)
(5)
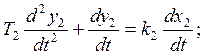 (6)
(6)
![]() (7)
(7)
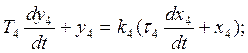 (8)
(8)
По полученным дифференциальным уравнениям запишем выражения передаточных функций:
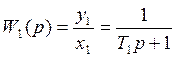 ;
;
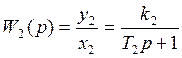 ;
;
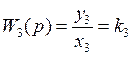 ;
;
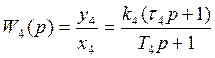 ;
;
Для наглядности впишем их в символы элементов на структурной схеме:
1.2. Преобразуем структурную схему к одноконтурной.
τ5 = k4*τ4 + T4 = 0.5
k5 = k4+1 = 1.5
τ6 = τ5/k5 = 0.333
k6 = k5*k3*k2 = 0.375
1.3. Определим передаточную функцию разомкнутой системы Wpaз(p).

k6 = k5*k3*k2 = 0.375 ;
 ;
;
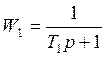
Передаточная функция разомкнутой системы:
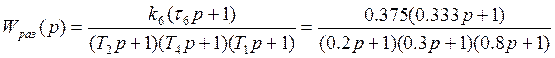
Коэффициент передачи разомкнутой системы:
![]()
1.4. Определим передаточные функции замкнутой системы по задающему ФXУ(р) и возмущающему ФZУ(р) воздействиям, запишем уравнения замкнутой системы в операторном и дифференциальном виде.
Передаточная функция замкнутой системы по управлению:
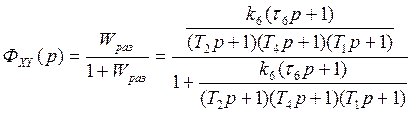
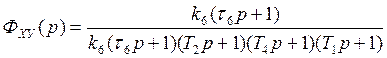
Передаточная функция замкнутой системы по возмущению:
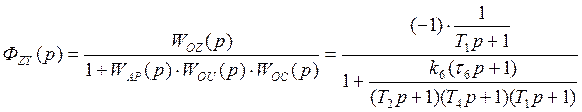
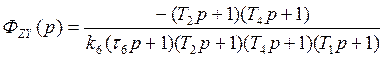
Уравнение замкнутой системы в операторной форме:
![]()
![]()
![]()
Уравнение замкнутой системы в дифференциальной форме:
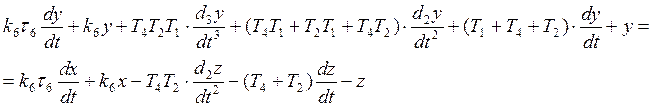
1.5. Проверим устойчивость по критерию Гурвица. По условию устойчивости определим предельное значение коэффициента передачи разомкнутой системы.
Запишем операторный полином при выходной координате Y в виде:
![]() ,
,
где
![]() ;
; ![]() ;
;
![]() ;
; ![]()
Для устойчивости системы необходимо чтобы все коэффициенты операторного полинома при Y были положительны. В нашем случае это условие выполняется:
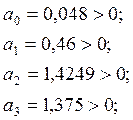
Для устойчивости
системы необходимо и достаточно, чтобы при всех ![]() все
диагональные миноры в определителе Гурвица были положительны, то есть
все
диагональные миноры в определителе Гурвица были положительны, то есть ![]() Подставим численные значения в достаточное
условие устойчивости системы:
Подставим численные значения в достаточное
условие устойчивости системы:
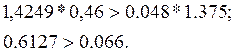
Достаточное условие устойчивости выполняется.
1.6. Вычислим установившиеся (статические) ошибки по задающему и возмущающему воздействиям, приняв для задающего воздействия ступенчатую и линейную функции, а для возмущающего – только ступенчатую функцию. Статические ошибки определяем в процентном отношении к модулю ступенчатого воздействия и скорости изменения линейного воздействия.
Передаточная функция ошибки по управлению:
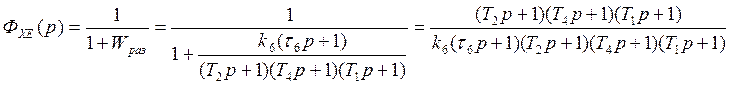
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.