Приближенные методы решения обыкновенных дифференциальных уравнений: Методические указания к выполнению лабораторной работы № 11, страница 2

где y^*_i и y_i – приближенные значения, полученные с шагом h/2  и h. Если ε – заданная точность решения, то число n (число делений) выбирается таким образом, чтобы h⁴< ε, т.е.

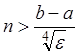                                                                                                                                               (11)

Методические указания

1.  Погрешность метода Эйлера рассчитывается из предположения, что точность метода Рунге-Кутта на много выше, и с точностью до четвертого десятичного знака погрешность расчета равна нулю. Исходя из этого предположения, E_i = |Y₂(x_i)-Y₁(x_i)|.

2.  Решение дифференциальных уравнений удобно оформить в виде соответствующих функций.

Пример написания программ

Задача: Решить дифференциальное уравнение на промежутке [1,6; 2,6] с шагом h=0,25 методом Эйлера и методом Рунге-Кутта. Начальные условия Xo=1,6; Yo=-4,6.

Program Eiler;

Uses CRT;

var   X, Y: array [0..20] of real;

      i, N: integer;

const A  = 1.6;  B  = 2.6;    { Диаппазон интегрирования X = [a,b]    }

      Xo = A;    Yo = -4.6;   { Начальные условия Yo = F(Xo)          }

      h  = 0.25;              { Шаг интегрирования h                  }

function F1(x,y: real): real; { Определяем функцию Y' = F(X, Y) }

begin

  F1:=x+cos(x/3)

end;

begin

  ClrScr;

  X[0]:=Xo; Y[0]:=Yo;         { Установка начальных значений (шаг i = 0) }

  N:= round((b-a)/h);

  for i:=1 to N do

  begin

    X[i]:=X[i-1]+h;

    Y[i]:=Y[i-1]+h*F1(X[i-1], Y[i-1]);

  end;

 writeln('i':5,'X':10,'Y':10);

 writeln('--------------------------------');

 for i:=0 to round((B-A)/h) do

     writeln(i:5,X[i]:10:4,Y[i]:10:4);

 writeln;

end.

Протокол выполнения программы

    i         X         Y

--------------------------------

    0    1.6000   -4.6000

    1    1.8500   -3.9847

    2    2.1000   -3.3183

    3    2.3500   -2.6021

    4    2.6000   -1.8374

Program Metod_Runge_Kutta; {Решение дифференциального уравнения методом Рунге-Кутта}

Uses CRT;

var   X, Y: array [0..20] of real;

      i: integer;

const A  = 1.6;  B  = 2.6;   { Диаппазон интегрирования X = [a,b]    }

      Xo = A;    Yo = -4.6;  { Начальные условия Yo = F(Xo)          }

      h  = 0.25;             { Шаг интегрирования h                  }

function F1(x,y: real): real; far; { Определяем функцию Y' = F(X, Y) }

begin

  F1:=x+cos(x/3)

end;

function DY(X,Y,h: real): real;  { Вспомагательная функция вычисления  }

var; K1, K2, K3, K4: real;       { элементарного приращения функции DY }

begin                            { на i-м шаге интегрирования методом  }

  K1:= h*F1(X,     Y);                       { Рунге-Кутта}

  K2:= h*F1(X+h/2, Y+K1/2);

  K3:= h*F1(X+h/2, Y+K2/2);

  K4:= h*F1(X+h,   Y+K3);

  DY:= (K1+2*K2+2*K3+K4)/6;

end;

begin

  ClrScr;    { Очистка экрана }

  X[0]:=Xo; Y[0]:=Yo;          { Установка начальных значений (шаг i = 0) }

  i:=1;                        { Переход на следующий шаг (i = 1) }

  while i<=round((B-A)/h) do   { Пока не пройдены все шаги ... }

  begin

    X[i]:=X[i-1]+h;                    { Увеличиваем X на величину шага h }

    Y[i]:=Y[i-1]+DY(X[i-1], Y[i-1], h);{ Вычисляем Yi }

    inc(i)                             { Увеличиваем номер шага на 1 }

  end;

  writeln('i':5,'X':10,'Y':10);

  writeln('-------------------------------');

  for i:=0 to round((B-A)/h) do

     writeln(i:5,X[i]:10:4,Y[i]:10:4);

end.

Протокол выполнения программы

    i         X         Y

-------------------------------

    0    1.6000   -4.6000

    1    1.8500   -3.9590

    2    2.1000   -3.2676

    3    2.3500   -2.5270

    4    2.6000   -1.7387

Контрольные вопросы

1.  Что представляет собой решение обыкновенного диф. уравнения?

2.  В чем заключаются преимущества и недостатки каждого метода решения дифференциальных уравнений?

3.  Как точность расчетов методом Эйлера зависит от шага интегрирования?

4.  Каким образом определяется погрешность расчетов в данной работе?

5.  Как на практике находят погрешность расчетов?

6.  От чего зависит точность решения дифференциальных уравнений?

Таблица 11.1 – Исходные данные

№	Уравнение	y0(a)	xÎ[a; b]	№	Уравнение	y0(a)	xÎ[a; b]
1		2,6	[1,8; 2,8]	16		2,2	[1,4; 2,4]
2		4,6	[1,6; 2,6]	17		2,5	[1,4; 2,4]
3		0,8	[0,6; 1,6]	18		1,3	[0,8; 1,8]
4		0,6	[0,5; 1,5]	19		1,5	[1,1; 2,1]
5		5,3	[1,7; 2,7]	20		1,2	[0,6; 1,6]
6		2,2	[1,4; 2,4]	21		1,8	[0,5; 1,5]
7		2,5	[1,4; 2,4]	22		1,1	[0,2; 1,2]
8		1,4	[0,8; 1,8]	23		0,8	[0,1; 1,1]
9		2,1	[1,2; 2,2]	24		0,6	[0,5; 1,5]
10		2,5	[2,1; 3,1]	25		1,4	[1,2; 2,2]
11		2,6	[2,8; 2,8]	26		0,8	[0,4; 1,4]
12		4,6	[1,6; 2,6]	27		0,9	[0,3; 1,3]
13		0,8	[0,6; 1,6]	28		1,8	[1,2; 2,2]
14		0,6	[0,5; 1,5]	29		2,1	[0,7; 1,7]
15		5,3	[1,7; 2,7]	30		1,7	[0,9; 1,9]