

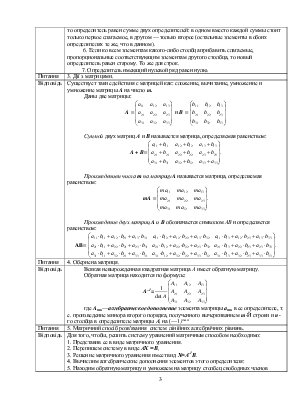



















если тогда их отнести к одному началу, то они все будут
лежать в одной плоскости (Р). Если а || b, то
представление с в виде линейной комбинации а и b
показано на (рис.149) оно называется разложением вектора в плоскости по
двум непараллельным векторам. Если же а || b, то согласно
предыдущему абзацу уже из двух векторов a, b один
(например, а) линейно выражается через другой (b), т.е. а
выражается через b и с.
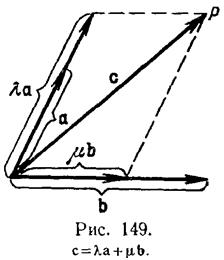
Четыре или более векторов всегда линейно зависимы. Действительно, пусть даны четыре вектора а, b, с, d; отнесем их к одному началу. Если после этого векторы а, b, с окажутся лежащими в одной плоскости, то по предыдущему абзацу один из них линейно выражается через остальные и т.д. (как в конце предыдущего абзаца). Пусть теперь а, b, с не лежат в одной плоскости (рис. 150). Тогда проводим через точку D(конец вектора d) прямую, параллельную вектору с до пересечения с плоскостью векторов а и b в точке С; затем через С проводим прямую, параллельную вектору b, до пересечения с прямой, на которой лежит вектор а, в точке В. Тогда
d =![]() =
=![]() а
+
а
+![]() b +
b + ![]() c. (1)
c. (1)
Это представление называется разложением
вектора по трем векторам, не параллельным одной плоскости; оно же
называется разложением вектора по трем осям (на рис. 150 по осям ii, mmи пп). Такое
разложение часто применяется в теоретической механике и в других дисциплинах
при разложении силы по трем направлениям и т.п. Каждое из слагаемых ![]() а,
а,![]() b и
b и ![]() c называется составляющей
или, что то же, компонентой вектора d по (вдоль)
соответствующей оси. Компонента вдоль каждой оси определяется не только
направлением этой оси, но и направлениями остальных осей. Однако от
ориентации осей, т.е. от указания на них положительного направления
компоненты не зависят.
c называется составляющей
или, что то же, компонентой вектора d по (вдоль)
соответствующей оси. Компонента вдоль каждой оси определяется не только
направлением этой оси, но и направлениями остальных осей. Однако от
ориентации осей, т.е. от указания на них положительного направления
компоненты не зависят.
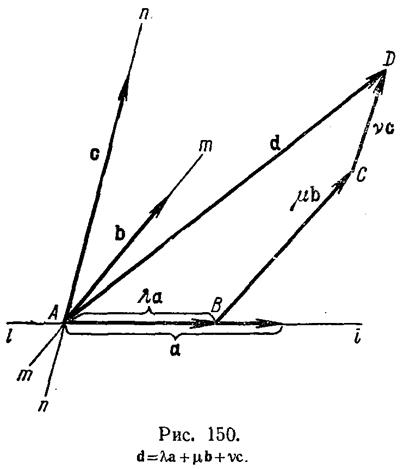
Иногда применяется разложение вектора по оси и не параллельной ей плоскости. Это разложение показано на рис. 151.
Разложение (1) возможно осуществить лишь единственным
образом. В самом деле, если бы наряду с (1) существовало другое разложение d= ![]() 1а +
1а +![]() 1 b +
1 b + ![]() 1
c , приравнивая правые части, мы получим (
1
c , приравнивая правые части, мы получим (![]() –
–![]() 1)а
+ (
1)а
+ (![]() –
–![]() 1)
b + (
1)
b + (![]() –
–![]() 1)c = 0, откуда вытекает линейная зависимость
векторов а, b, с (почему?). Если
дано более четырех векторов, то уже из первых четырех векторов один линейно
выражается через все остальные, т.е. векторы линейно зависимы.
1)c = 0, откуда вытекает линейная зависимость
векторов а, b, с (почему?). Если
дано более четырех векторов, то уже из первых четырех векторов один линейно
выражается через все остальные, т.е. векторы линейно зависимы.
Питання
3. Базис на площині і у просторі.
Відповідь
Совокупность линейно независимых векторов, по которым производится разложение остальных векторов, называется базисом. В плоскости базисом могут служить любые два непараллельных вектора, а в пространстве – любые три вектора, не параллельных одной плоскости.
Питання
4. Проекція вектора на вісь. Властивості проекцій.
Відповідь
Выражение «проекция вектора ![]() на ось ОХ» употребляется в двух
разных смыслах: геометрическом и алгебраическом (арифметическом).
на ось ОХ» употребляется в двух
разных смыслах: геометрическом и алгебраическом (арифметическом).
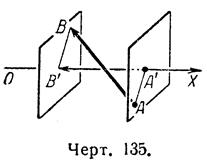
1. Проекцией (геометрической) вектора![]() на ось ОХ называется вектор
на ось ОХ называется вектор ![]() (черт. 135), начало которого А' есть
проекция начала А на ось ОХ, а конец В' – проекция конца
В на ту же ось.
(черт. 135), начало которого А' есть
проекция начала А на ось ОХ, а конец В' – проекция конца
В на ту же ось.
Обозначение: Прox![]() или, короче, Пр
или, короче, Пр ![]() .
.
Если ось ОХ задана вектором с, то
вектор ![]() называется также проекцией вектора
называется также проекцией вектора ![]() на направление вектора с и
обозначается Прc
на направление вектора с и
обозначается Прc![]() .
.
Геометрическая проекция вектора на ось ОХ называется также компонентой вектора по оси ОХ.
2. Проекцией (алгебраической) вектора ![]() на ось ОХ (или на
направление вектора с) называется длина вектора
на ось ОХ (или на
направление вектора с) называется длина вектора![]() взятая
со знаком + или –, смотря по тому, имеет
взятая
со знаком + или –, смотря по тому, имеет
ли вектор![]() то же
направление, что ось ОХ (вектор с), или противоположное. Обозначение:
прox
то же
направление, что ось ОХ (вектор с), или противоположное. Обозначение:
прox![]() или прc
или прc![]() .
.
Замечание. Геометрическая проекция (компонента) вектора есть вектор, а алгебраическая проекция вектора есть число.
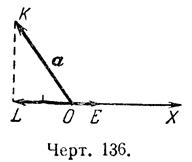
Пример 1. Геометрическая проекция вектора ![]() =а (черт.136) на ось ОХ есть
вектор
=а (черт.136) на ось ОХ есть
вектор ![]() . Его направление противоположно
направлению оси, а длина (при единице масштаба ОЕ) равна 2. Значит,
алгебраическая проекция вектора
. Его направление противоположно
направлению оси, а длина (при единице масштаба ОЕ) равна 2. Значит,
алгебраическая проекция вектора![]() а ось ОХ есть
отрицательное число —2; Пр
а ось ОХ есть
отрицательное число —2; Пр ![]() =
=![]() , пр
, пр ![]() = —2.
= —2.
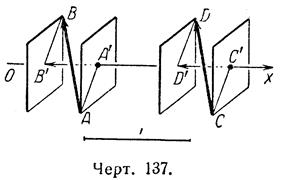
Если векторы![]() и
и ![]() (черт.137)
равны, то их алгебраические проекции по одной и той же оси тоже равны (пр
(черт.137)
равны, то их алгебраические проекции по одной и той же оси тоже равны (пр![]() = пр
= пр![]() =
= ![]() ). То же для геометрических проекций.
). То же для геометрических проекций.
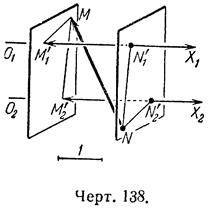
Алгебраические проекции одного и того же вектора на две разнонаправленные оси (О1Х1 и О2Х2 на (черт.138) равны (Если оси параллельны, но противоположно направлены, то алгебраические проекции не равны; они отличаются знаком
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.