Определение числовых характеристик отдельных выборок. Критерий Вилькоксона и проверка гипотезы об однородности двух выборок. Сравнение двух дисперсий нормальных генеральных совокупностей (критерий Фишера), страница 3

Если |Z_набл| < z_кр – нет оснований отвергнуть нулевую гипотезу. Если |Z_набл| > z_кр - нулевая гипотеза отвергается.

2.  Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки) (Критерий Стьюдента)

Допустим, имеются две малые независимые выборки объемом n и m (n≤30, m≤30), по которым найдены соответствующие выборочные средние -  и дисперсии.

Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H₀: М(Х₁)=M(X₂) о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае малых независимых выборок) при конкурирующей гипотезе Н₁: M(X₁) ≠M(X₂), надо вычислить наблюдаемое значение критерия

,

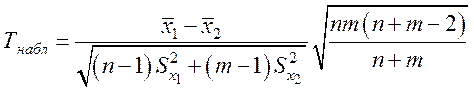и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, (таблица приложения 2), и числу степеней свободы k=n+m-2 найти критическую точку двухстороннего критерия t_{двуст.кр.}(α,k). Если |Т_набл|<t_{двуст.кр.}(α,k) – нет оснований отвергать нулевую гипотезу, в противном случае, нулевую гипотезу отвергают.

3.  Сравнение двух дисперсий нормальных генеральных совокупностей
(критерий Фишера)

Если необходимо сравнить две дисперсии , двух независимых выборок, объемы которых n и m.

Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу Н₀: D(X₁) = D(X₂) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H₁: D(X₁)>D(X₂), необходимо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)

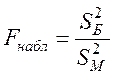
и по таблице критических точек распределения Фишера, по заданному уровню значимости α и числам степеней свободы k₁ = n-1, k₂ = m-1 (k₁ – число степеней свободы большей исправленной дисперсии) найти критическую точку F_кр(α; k₁, k₂). Если F_набл <F_кр – нет оснований отвергнуть нулевую гипотезу. Если F_набл>F_кр – нулевую гипотезу отвергают.

Решение:

Проверить гипотезы о равенстве средних и дисперсий для двух выборок Х₁ и Х₂, при уровне значимости α=0,01.

Так как в нашем распоряжении выборки объемами n = 20 и m = 20 (малые выборки), то для проверки гипотезы о равенстве математических ожиданий воспользуемся критерием Стьюдента.

Из предыдущего примера известны:= 9,656 , = определим наблюдаемое значение критерия T:

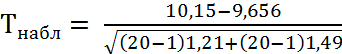
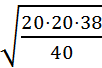            = 1,345

Число степеней свободы: k=20+20-2 = 38.  По уровню значимости α = 0,01 и числу степеней свободы определяем критическую точку t_{двуст.кр}(0.01;38) = 2.11.

Так как Т_набл< t_{двуст.кр}(0.01;38), следовательно нет оснований отвергать нулевую гипотезу о равенстве средних, или различные значения средних из двух выборок различаются статистически незначимо.

Для проверки гипотезы о равенстве двух выборочных дисперсий, найдем отношение большей дисперсии к меньшей:

                                  = = 1.23

Число степеней свободы для первой и второй выборки: k₁ = k₂ = 19. Критическая точка распределения Фишера при уровне значимости α = 0,01 – F_кр(0.01; 19, 19) = 3.0.

Так как F_набл< F_кр(0.01;19), следовательно, нет оснований отвергать нулевую гипотезу о равенстве дисперсий, или различные значения дисперсий из двух выборок различаются статистически незначимо.

4.Построение эмпирической функции распределения
по статистическим данным.

Эмпирической функцией распределения (функцией распределения выборки), называют функцию F*(x), определяющую для каждого значения x относительную частоту события X < x:

F*(x) = n_x/n,

где n_x  - число вариант (измерений, чисел в таблице), меньших х,

n – объем выборки.

Эмпирическая функция обладает следующими свойствами.

Свойство 1. Значения эмпирической функции принадлежит отрезку [0, 1].

Свойство 2. F*(x) – неубывающая функция.

Свойство 3. Если х₁ – наименьшая варианта, а x_k – наибольшая варианта, то F*(x) = 0, при х≤х₁ и F*(x) = 1 при х>x_k.

Рассмотрим на примере выборки Х₁ построение эмпирической функции распределения. Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной X, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюденных значений m_i, приходящиеся на каждый i– й интервал.