Интегральное исчисление функций одной переменной

Контрольная работа № 3

Интегральное исчисление функций одной переменной.

Для успешного выполнения контрольной работы № 3 необходимо внимательно изучить следующие теоретические вопросы:

4.1. Неопределенный интеграл.

1.  Основная задача интегрирования.

2.  Понятие первообразной функции.

3.  Понятие неопределенного интеграла. Его свойства.

4.  Таблица интегралов.

5.  Методы интегрирования: а) непосредственное (табличное) интегрирование; б) интегрирование по частям; в) интегрирование заменой переменной.

6.  Интегрирование рациональных дробей. Разложение правильной рациональной дроби на простейшие. Интегрирование простейших дробей 1, 2, 3 типа.

7.  Интегрирование тригонометрических функций:

а) ;

б)

в)

г)

д) ;

е) , , .

8.  Интегрирование иррациональных функций:

а) , ;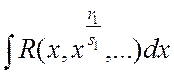

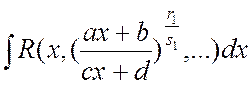б) , ,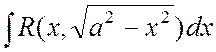

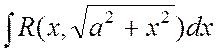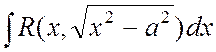
9.  Не берущиеся интегралы.

4.2. Определенный интеграл.

1.  Задача о площади криволинейной трапеции.

2.  Определение определенного интеграла.

3.  Свойства определенного интеграла.

4.  Вычисление определенного интеграла. Формула Ньютона – Лейбница.

5.  Интегрирование по частям и заменой переменной в определенном интеграле.

6.  Несобственные интегралы I и II рода. Их определение, сходимость и расходимость.

7.  Вычисление площади плоской фигуры, длины дуги кривой, объема тела вращения, если кривая задана:

а) явно,

б) параметрически,

в) в полярных координатах.

Таблица основных неопределенных интегралов.

1. 

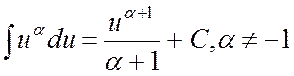
2. 

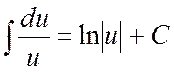
3. 

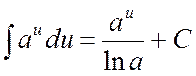
4. 

5. 

6. 

7. 

8. 

9. 

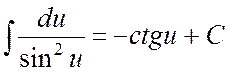
10. 

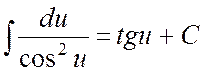
11. 

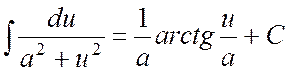
12. 

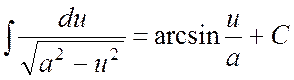
13. 

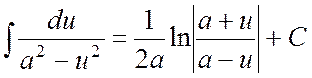
14. 

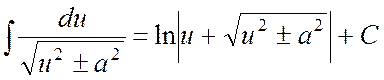
Отыскание неопределенного интеграла с помощью приведенной таблицы и тождественных преобразований подынтегрального выражения называется непосредственным интегрированием. Следует иметь в виду, что в таблице u – функция от x, т. е. u = u (x), тогда .

Примеры решения задач.

Пример 1. Найти интеграл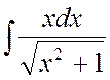

Ñ Удобно представить 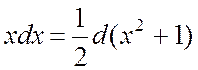. Тогда

.

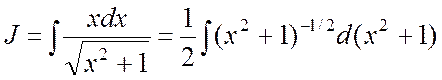Здесь . По формуле (1) таблицы имеем:

. #

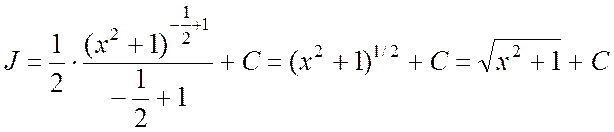Пример 2. Найти интеграл .

Ñ . Здесь , , использовалась формула (5). #

Пример 3. Найти интеграл .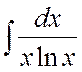

Ñ 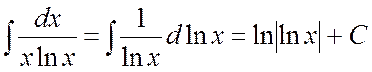. Здесь 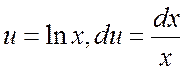, использовалась формула (2). #

Пример 4. Найти интеграл .

Ñ Чтобы найти этот интеграл, применим формулу интегрирования по частям:

                                           (4.1)

Обозначим: . Удобно использовать следующую запись:

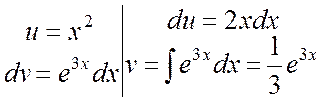
Тогда 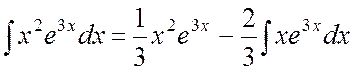. Еще раз применим формулу (4.1):

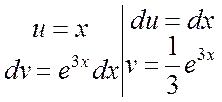
Следовательно, имеем:

. #

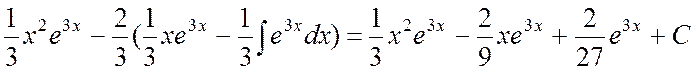Пример 5. Найти интеграл .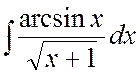

Ñ Для нахождения интеграла применим формулу (4.1):

. #

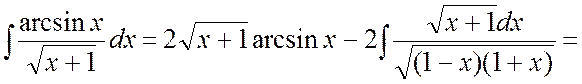
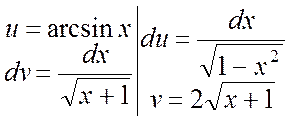
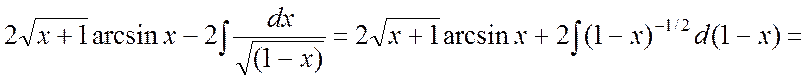
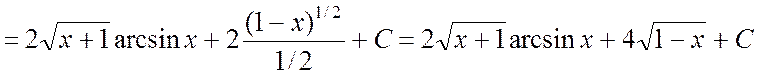Пример 6. Найти интеграл .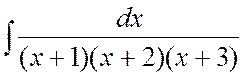

Ñ Под интегралом стоит правильная рациональная дробь. Чтобы найти этот интеграл, подынтегральную дробь нужно представить в виде суммы элементарных дробей. Это представление зависит от разложения знаменателя на множители. Корни знаменателя действительные простые, а именно x₁ = -1, x₂ = -2, x₃ = -3. Тогда

.

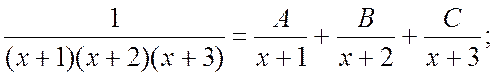
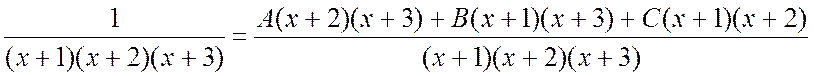Отсюда . Полагая последовательно x = -1, x = -2, x = -3, получим:

. #

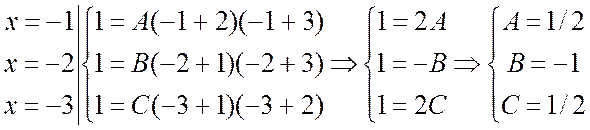
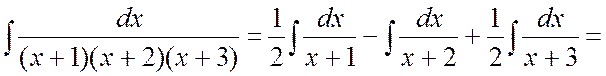
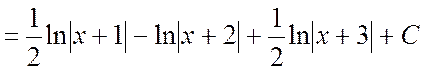Пример 7. Найти интеграл .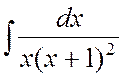

Ñ Подынтегральная функция представляет собой правильную рациональную дробь. Корни знаменателя: x₁ = 0 – простой действительный, x₂ = -1 – действительный кратности 2. Следовательно, разложение этой дроби на элементарные выглядит так:

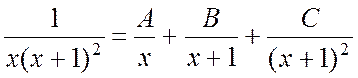
                                 (4.2)

Положим x = 0 и x = -1, получим два уравнения:

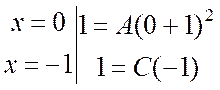
Приравнивая коэффициенты при x² слева и справа в уравнении (4.2), получим и третье уравнение:

Итак, имеем систему уравнений относительно A,B,C:

. #

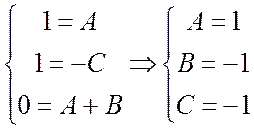
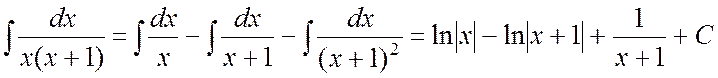Пример 8. Найти интеграл .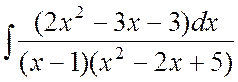

Ñ Под интегралом - правильная рациональная дробь. Знаменатель имеет следующие корни: x₁ = 1 – простой действительный,  - пара простых комплексных сопряженных. Подынтегральная дробь разлагается на элементарные следующим образом:

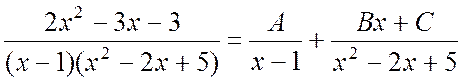
                (4.3)

Полагая x = 1 и приравнивая коэффициенты при x₂ и x₀ слева и справа в равенстве (4.3), будем иметь систему уравнений:

. #

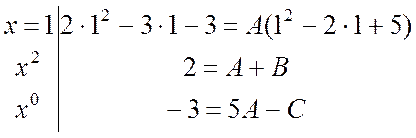
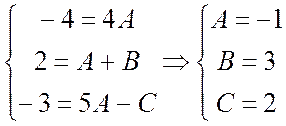
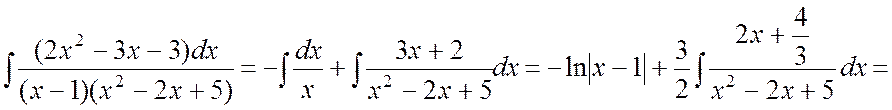
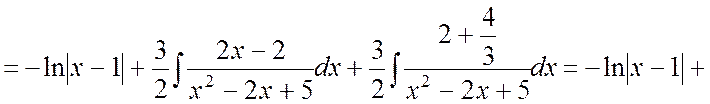
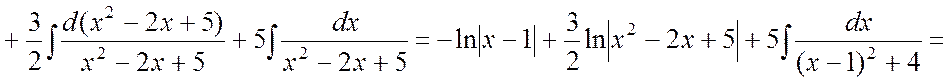
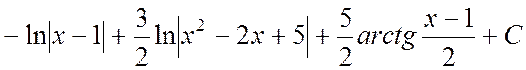Пример 9. Найти интеграл .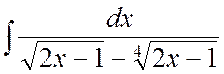

Ñ Под интегралом стоит иррациональная функция вида:

.

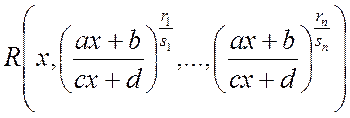Здесь a = 2; b= -1; c = 0; d= 1; 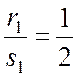;  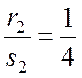. Сделаем подстановку , т. к. 4 – наибольший знаменатель дробей   и  , следовательно, , . Отсю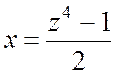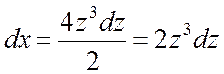да , . Тогда

. #

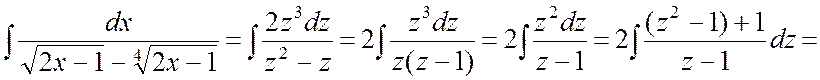
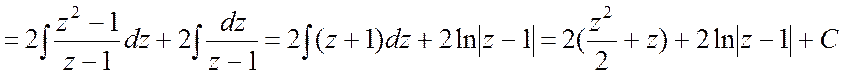
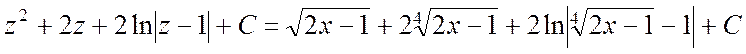Пример 10. Найти интеграл .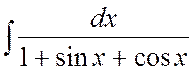

Ñ Сделаем подстановку 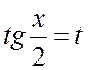, тогда , , .

. #

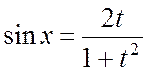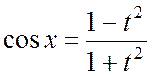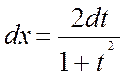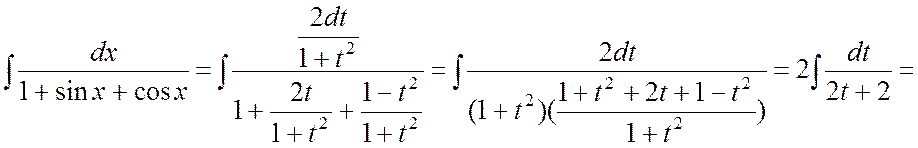
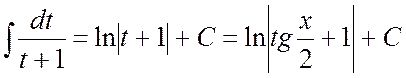Замечание: Если интеграл находится с помощью какой-либо подстановки (заменой переменной), то в конце нужно обязательно вернуться к старой переменной.

Пример 11. Вычислить несобственный интеграл или доказать его расходимость: .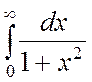

Ñ Дан несобственный интеграл I рода. Он определяется как предел соответствующего определенного интеграла:

.

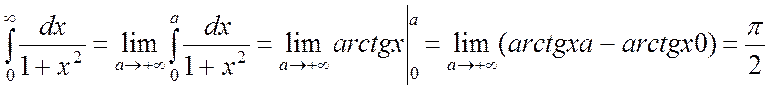Так как предел получился конечный, то интеграл сходится. #

Пример 12. Вычислить несобственный интеграл или доказать его расходимость: .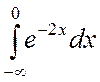

Ñ Дан несобственный интеграл I рода. Определим его как предел соответствующего определенного интеграла:

.

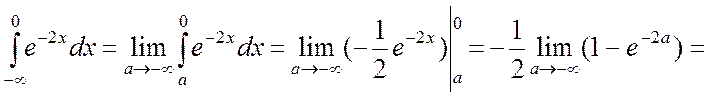
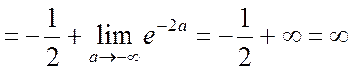Следовательно, интеграл расходится.

Пример 13. Вычислить несобственный интеграл или доказать его расходимость: .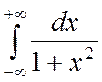

Ñ Данный несобственный интеграл определяется как сумма двух интегралов: