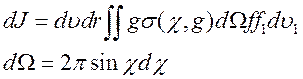 (6.31).
(6.31).
Аналогично, для частиц покидающих фазовый объем в результате столкновений получим выражение потока
![]() (6.32).
(6.32).
Тогда столкновительный член запишется
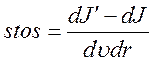 или с учетом того, что
или с учетом того, что
![]()
![]() (6.33).
(6.33).
Уравнение (6.29) со столкновительным членом (6.33)
называется кинетическим уравнением Больцмана. Оно описывает процесс перехода
системы из неравновесного состояния в равновесное, является нелинейным
интегродифференциальным уравнением и в общем случае решение его не найдено.
Заметим, что равновесная функция распределения Максвелла-Больцмана является
решением уравнения (6.29) при ![]() (она обращает
столкновительный член в нуль). Известные решения уравнения Больцмана получены
только для случаев, когда функция распределения мало отклоняется от
равновесной, т. е. в предположении малости параметров, приводящих к отклонению
системы от состояния равновесия. В этом случае искомую функцию представляют в
виде:
(она обращает
столкновительный член в нуль). Известные решения уравнения Больцмана получены
только для случаев, когда функция распределения мало отклоняется от
равновесной, т. е. в предположении малости параметров, приводящих к отклонению
системы от состояния равновесия. В этом случае искомую функцию представляют в
виде:
![]() (6.34),
(6.34),
где ![]() малая величина. Подставляя
(6.34) в (6.33) и далее в (6.29), с точностью до малых первого порядка будем
иметь
малая величина. Подставляя
(6.34) в (6.33) и далее в (6.29), с точностью до малых первого порядка будем
иметь
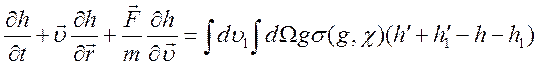 (6.35).
(6.35).
Это уже линейное интегродифференциальное уравнение и имются
методы его решения. В качестве примера рассмотрим еще более упрощенную модель,
когда функция распределения ![]() мало отличается от
равновесной
мало отличается от
равновесной ![]() и столкновительный член представляется в
виде
и столкновительный член представляется в
виде 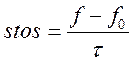 , где
, где ![]() время
релаксации – время, в течении которого система приходит в состояние равновесия.
Эта модель получила название “
время
релаксации – время, в течении которого система приходит в состояние равновесия.
Эта модель получила название “![]() приближение”. Из опыта
известно, что в газе достаточно нескольких столкновений чтобы установилась
Максвелловская функция распределения по скоростям и следовательно
приближение”. Из опыта
известно, что в газе достаточно нескольких столкновений чтобы установилась
Максвелловская функция распределения по скоростям и следовательно ![]() , где
, где ![]() средняя
частота столкновений.
средняя
частота столкновений.
Проиллюстрируем использование этого приближения на
примере стационарной плазмы при наличии малого градиента температуры. Совместим
ось х с направлением градиента температуры, тогда уравнение Больцмана в ![]() приближении для электронной функции
распределения есть
приближении для электронной функции
распределения есть
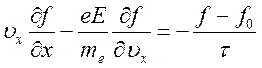 (6.36).
Здесь
(6.36).
Здесь ![]() собственное электрическое поле, связанное с
наличием градиента температуры и имеющее тот же порядок малости. Поскольку
собственное электрическое поле, связанное с
наличием градиента температуры и имеющее тот же порядок малости. Поскольку ![]() , где
, где 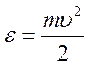 .
Тогда
.
Тогда 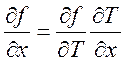 и из (6.36) получаем
и из (6.36) получаем
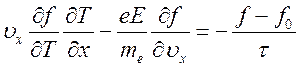 (6.37).
(6.37).
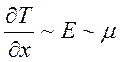 , где
, где ![]() малый
параметр и представим искомую функцию распределения в виде разложения по этому
малому параметру
малый
параметр и представим искомую функцию распределения в виде разложения по этому
малому параметру
![]() (6.38).
(6.38).
Подставим разложение (6.38) в (6.37) и с точностью до малых второго порядка получим
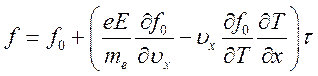 (6.39).
(6.39).
Возьмем в качестве ![]() функцию распределения
Максвелла
функцию распределения
Максвелла 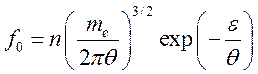 , где приняты обозначения:
, где приняты обозначения: 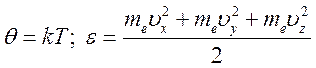 . Тогда
. Тогда 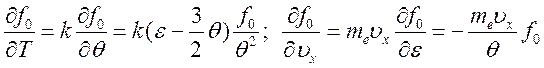 и
искомая функция распределения примет вид
и
искомая функция распределения примет вид
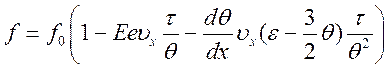 (6.40).
(6.40).
Определим плотность электрического тока и поток тепла
![]() (6.41).
(6.41).
![]() (6.42).
(6.42).
После подстановки (6.40) в (6.41) и (6.42) получим
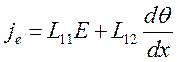 (6.43),
(6.43),
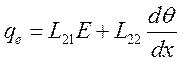 (6.44),
(6.44),
где
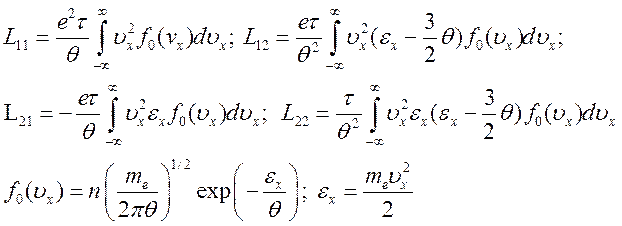 (6.45).
(6.45).
Коэффициенты ![]() называются
коэффициентами взаимности Онзагера. Непосредственные вычисления (6.45) дают
называются
коэффициентами взаимности Онзагера. Непосредственные вычисления (6.45) дают
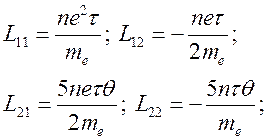 (6.46).
(6.46).
Из (6.43) следует, что коэффициент ![]() ,
стоящий перед напряженностью электрического поля
,
стоящий перед напряженностью электрического поля ![]() , есть
проводимость плазмы
, есть
проводимость плазмы 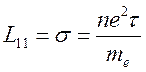 , что с учетом
, что с учетом ![]() совпадает с полученным ранее выражением
(4.38).
совпадает с полученным ранее выражением
(4.38).
Из условия, что в стационарном режиме при отсутствии внешнего электрического поля ток в плазме равен нулю будем иметь
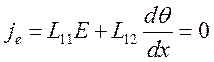 (6.47),
откуда
(6.47),
откуда
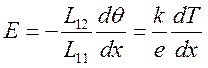 ,
, 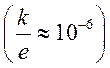 (6.48),
(6.48),
что находится в соответствии со сделанным в начале предположением. С учетом (6.48) выражение (6.44) для потока тепла запишется
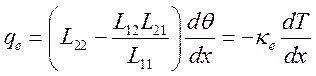 (6.49),
(6.49),
где коэффициент электронной теплопроводности ![]() есть
есть
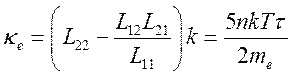 (6.50),
(6.50),
который (с точность до числового множителя) совпадает с выражением, следующим из элементарной кинетической теории.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.