Термодинамика и равновесный состав химически реагирующего газа, страница 2

Статистическая сумма по электронным состояниям:

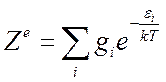                                                                   (7.18),

 – энергия  уровня,  – статистический вес этого уровня.

          Найдем определяющую систему для расчета состава газа в равновесной химической реакции, для чего воспользуемся условием равновесия

                                                                       (7.19).

Используя выражение  свободной энергии (7.13), из (7.19) находим:

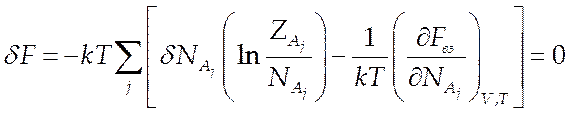                                        (7.20).

Заменяя  пропорциональными им величинами стехиометрических коэффициентов , получим

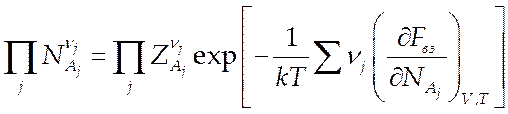                                                 (7.21).

          Уравнение (7.21) есть универсальное уравнение равновесия для системы, в которой идут произвольные реакции, с учетом слабого взаимодействия.

 Учет взаимодействия при нормальных плотностях необходим лишь для дальнодействующих потенциалов – при рассмотрении ионизационного равновесия. Для реакции в среде нейтральных частиц взаимодействие становится заметным при давлениях .

Диссоциация двухатомных молекул.

При температурах порядка нескольких тысяч градусов Кельвина двухатомные молекулы обычно диссоциируют на атомы. Многоатомные молекулы, в которых связь слабее, начинают распадаться при более низких температурах. Рассмотрим реакцию диссоциации двухатомных молекул типа

 или                                                           (7.22).

Запишем условие сохранения числа частиц

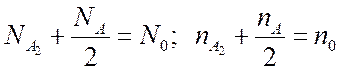                                                     (7.23),

где  начальное число молекул (начальное число молекул в единице объема). Определим степень диссоциации как

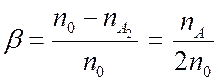;                                                                     (7.24).

Из (7.23) и (7.24) имеем, . Запишем уравнение состояния диссоциирующего газа

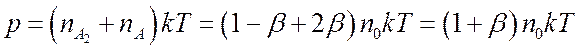                    (7.25)

или

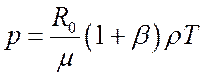                                                                        (7.26).

Удельная (на единицу объема) внутренняя энергия газа будет:

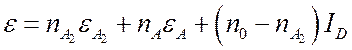                                                   (7.27).

Здесь  - есть средние значения энергии поступательного, вращательного и колебательного видов движения соответственно, а  - среднее значение энергии  по электронным состояниям частицы. 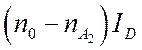  - энергия, затрачиваемая на диссоциацию,  - потенциал диссоциации. Например, для молекул кислорода , азота , окиси азота .

С учетом (7.23) и (7.24) выражение (7.27) запишется

                                             (7.28).

Обычно диссоциация начинается при температурах гораздо меньших чем . Это связано с тем, что при  молекулы разбиваются ударами очень энергичных частиц из «Максвелловского хвоста» распределения.

Для реакции (7.22)  и при  из (7.21) находим

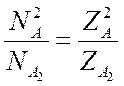                                                                                   (7.29).

Поскольку статистические суммы пропорциональны объему , который входит только в , а, в остальном, зависят только от температуры, то переходя к концентрациям  вместо (7.29) можно записать

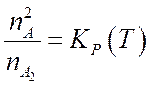                                                                                (7.30).

 есть константа равновесия для реакции диссоциации. Подставим в (7.29) значения статистических сумм из (7.15) – (7.18). В  положим 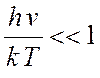 (колебания в молекулах возбуждены полностью), тогда 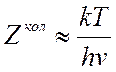, а в электронных суммах ограничимся первыми членам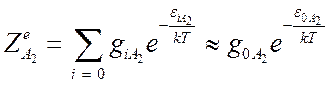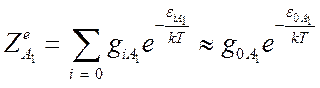и:

,   и 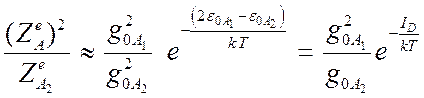 , так как разность энергии низких уровней  по определению есть энергия диссоциации .

В итоге для константы равновесия с учетом, что 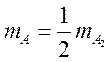 получим

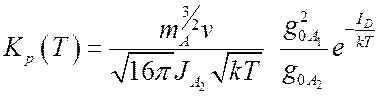                                               (7.31).

Переходя в (7.30) от  к степени диссоциации  и плотности  получим

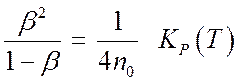                                                                   (7.32).

Используя уравнение состояния (7.26), из (7.32) можно получить

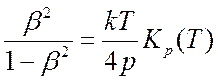                                                            (7.33).

При малых степенях диссоциации 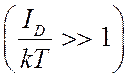 будем иметь  и степень диссоциации быстро (как экспонента) возрастает с повышением температуры, что влечет за собой резкое возрастание теплоемкости .

Расчет состава в случае произвольной химической реакции.

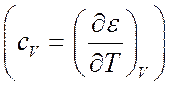Описанный выше подход может быть применен к любым химическим реакциям. Рассмотрим, например, химическое равновесие реакции типа . Типичная реакция этого типа - окисления азота , эта реакция идет при не слишком высоких температурах , когда диссоциация молекул  и  еще мала и ею можно пренебречь. Пусть в исходной смеси содержится  и  молекул  и . Сответствующие величины, отвечающие мгновенным значениям при заданных  и , есть , , и продукта реакции . Число молекул связаны между собой условием сохранения числа частиц

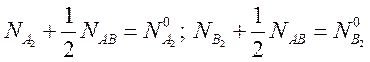                                                (7.34).

Обозначим , ,  - энергии одной молекулы, а через  - тепловой эффект реакции – энергия, выделяющаяся при превращениях двух молекул  и  в две молекулы  (если реакция идет с поглощением тепла, то ). Тогда внутренняя удельная энергия газа есть:

, где .

Как и раньше, определяя минимум свободной энергии по переменным , ,  получим:

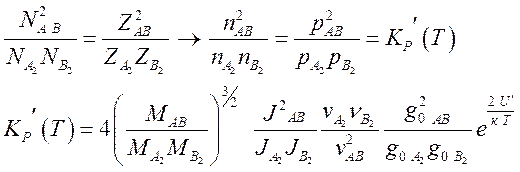                           (7.35).

Множитель 4 в константе равновесия возник от отношения факторов симметрии 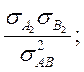  где (см. (7.16))

Если газ представляет собой смесь, в которой протекает целый ряд реакции, то для каждой реакции из закона действующих масс и сохранения числа частиц можно получить формулы типа (7.35), которые образуют систему нелинейных алгебраических уравнений, определяющих химический состав. Как было показано Я. Б. Зельдовичем, эта система имеет единственное решение, то есть равновесный химический состав определяется однозначно и далее на основе выражения для свободной энергии можно рассчитать все термодинамические величины газовой смеси.