Структура молекул. Гибридизация, страница 2

 - полный момент молекулы без учета спина не сохраняется даже приближенно.

Энергия в случае (б): 

 .

          Без учета спин-орбитального взаимодействия для нахождения энергии можно использовать выражение:

,        где  = 0,1,2...

          Спин-орбитальная добавка имеет вид оператора, который должен быть усреднен по электронному и вращательному состояниям при заданном R (расстоянии между ядрами).

 ,

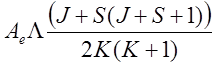где А_е - некоторая функция расстояния между ядрами при R = R₀.

Порядок величин колебательной и вращательной энергии.

Молекула СО :  М = 1,14·10 кг, расстояние между атомами 0,113 нм и I = 1,46·10 кг·м².

Минимальная энергия вращения (J = 1) равна  ~ 5·10 эВ.

Угловая скорость вращения .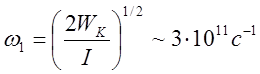

Колебательная энергия молекулы СО :,

частота колебаний .

Электронные спектры двухатомных молекул

Правила отбора для дипольных переходов:

 ,

причем для двух  термов:  .

 Для гомоядерных молекул выполняется правило:  .

диссоциация. Происходит возбуждение электронного состояния 2 и переход без изменения энергии в нестабильное состояние 3.

2.7.  Электронные спектры двухатомных молекул

Расстояние между электронными уровнями энергий () существенно больше колебательных и, тем более, вращательных уровней энергии. При электронном переходе изменяется конфигурация электронной оболочки и, следовательно, изменяются силы притяжения между ядрами, колебательные и вращательные движения ядер. Поэтому, при электронных переходах изменяется вращательно-колебательное состояние молекулы.

          Электронный переход происходит за малую долю времени колебания молекулы (скорость электронов велика по сравнению со скоростью ядер). Поэтому можно считать, что во время перехода взаимное расстояние и импульс ядер остается неизменным (принцип Франка - Кондона). Для электронного спектра молекул наиболее существенны (как и в атомах) электрические дипольные переходы, подчиняющиеся следующим правилам отбора:

 ,                            (90)

причем для двух  термов:  .  Для гомоядерных молекул выполняется правило:  .

          При анализе электронных переходов не существует никакого правила отбора для квантового числа , характеризующего колебательное состояние. Переход осуществляется по специальному правилу (принципу), который мы пояснили ниже.

          На рис. 23 показана зависимость энергии молекул Е = W_e + W_K от расстояния между атомами. На больших расстояниях взаимодействие мало и энергия системы определяется энергией отдельных атомов. На малых расстояниях сильно кулоновское отталкивание ядер. На расстоянии R₀ зависимостьW_e  от  R имеет минимум, то есть реализуется устойчивое состояние молекулы. Таким образом, функция W₀(R) имеет форму потенциальной ямы.

          Учет движения ядер обуславливает появление дополнительной положительной энергии W_K , уровни которой показаны на рис. 23. Полная энергия молекулы увеличивается. На рис 23 на каждом электронно-колебательном уровне показано распределение плотности вероятности  для соответствующей волновой функции гармонического осциллятора. В колебательно-возбужденных состояниях  плотность вероятности нахождения атомов увеличивается у границ потенциальной ямы, то есть у точек поворота. Хорошо известно, что вблизи точек поворота проводит значительную долю времени любая колеблющаяся система.

          По принципу Франка - Кондона электронный переход совершается при постоянном расстоянии между ядрами. Это означает, что переход с максимальной вероятностью может осуществляться при условии максимума произведения вероятностей пребывания атома на соответствующем участке колебательной траектории верхнего и нижнего уровней. Практически это означает, что переходы осуществляются между теми колебательными состояниями, у которых максимумы  лежат на одном R.

          На рис. 24a,б,в показаны три характерные ситуации, иллюстрирующие эти правила отбора переходов. Нижние потенциальные кривые относятся к основному электронному состоянию молекулы. Верхние - к возбужденному. Видно, что смещение потенциальных кривых приводит к тому, что с нулевого колебательного уровня  возбуждаются все более высокие колебательные состояния верхнего электронного терма.

          Если потенциальные кривые (рис. 24г) пересекаются, причем одна из них  соответствует  распадному состоянию, то  возможна пре-

Рис. 23.  Электронно-колебательная энергия. Колебательные

                       уровни. Плотность вероятности  для различных

                       колебательных состояний u = n.

Рис. 24.  Схемы реализации отбора переходов по принципу

                          Франка-Кондона и предиссоциации.

Рис. 25.  Схема электронных термов молекул N₂, .

Рис. 26.  Теоретические кривые электронных термов Не₂ и .

диссоциация. Происходит возбуждение электронного состояния 2 и переход без изменения энергии в нестабильное состояние 3.

          На рис. 25, 26 в качестве примера приведены схемы электронных термов молекул . Напомним, что молекула Не₂  устойчива только в возбужденном состоянии.