Столкновительные процессы в плазме, страница 4

          В большинстве случаев коэффициенты переноса определяются в основном упругими столкновениями с рассеянием на большие углы. В связи с этим среднюю частоту столкновении в приближении Чепмена – Энскога кинетической теории определяют следующим образом:

          ,                                                                                        (3.36)

где  - среднее сечение столкновения с передачей импульса, определяемое выражением

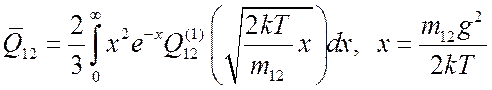          ,                                        (3.37)

а величина

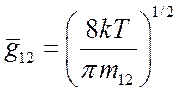                                                                                               (3.38)

есть средняя относительная скорость частиц с максвелловским распределением по скоростям. В случае, когда сечение столкновения медленно меняется вблизи , можно воспользоваться приближенным соотношением

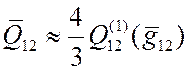.                                                                                   (3.39)

Формулы (3.36) и (3.37) можно рассматривать как определение среднего (с энергетическим весом) значения зависящей от скорости частоты столкновений с передачей импульса. Не трудно убедится, что

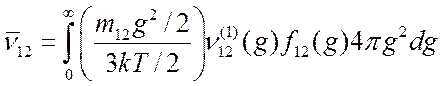          .                                               (3.40)

Здесь  , а  - максвелловская функция распределения.

Передача энергии и импульса при упругом столкновении

         При упругом столкновении двух частиц их суммарная кинетическая энергия не меняется, в то время как скорости самих частиц в любой системе отсчета, кроме системы, движущейся со скоростью центра масс двух частиц, меняются.

           Рассмотрим столкновение двух частиц в газе в системе координат, движущейся со средней массовой скоростью . Обозначим скорости частиц в указанной системе отсчета до столкновения через  и . Столкновение частиц приводит к рассеянию, описываемому углами  (рис. (3.2)). Согласно формуле (3.34), скорости падающей частицы до и после столкновения запишутся

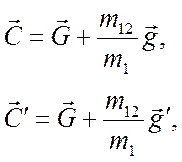                                                                                               (3.41)

          Энергия, теряемая падающей частицей в процессе столкновения, определяется следующим образом:

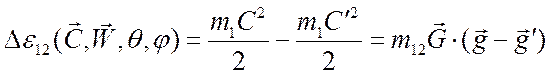          .                                (3.42)

Произведя усреднение по всем углам рассеяния, получим

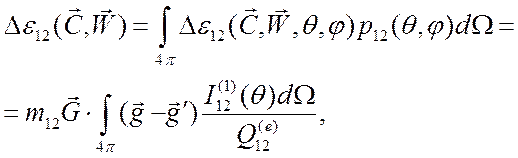                                               (3.43)

где  - вероятность упругого рассеяния в элемент телесного угла , определяемого формулой (3.6). Вычисление интеграла в правой части (3.43) с учетом выражения (3.4) дает

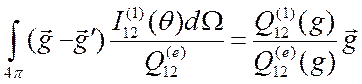 и .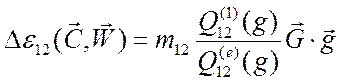

Используя соотношения (3.33), получаем окончательно

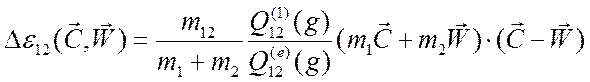          .                          (3.44)

          Рассмотрим сначала частный случай, когда частица-мишень покоится, т.е. . Тогда из формулы (3.44) следует, что

          .

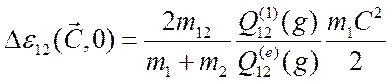Таким образом, средняя доля начальной кинетической энергии, теряемой падающей частицей на покоящеюся частицу-мишень со скоростью С, равна

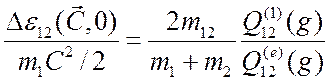          .                                                               (3.45)

Этот результат чаще всего применяется к столкновениям, в которых падающей частицей является электрон, а частицей-мишенью - тяжелая частица (атом, ион, молекула).. Поскольку ,получим

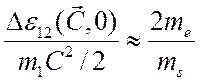          ,                                                                                  (3.46)

где  - масса тяжелой частицы. То обстоятельство, что отношение масс в правой части равенства (3.46) мало, означает, что в некоторых случаях энергообмен между частицами может быть незначительным. В подобных случаях вводится понятие температуры электронов  отличной от температуры тяжелых частиц .

          Вернемся к формуле (3.44) и вычислим энергию, теряемую падающей частицей, усредненную по скоростям всех частиц-мишеней

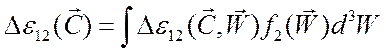          .                                                       (3.47)