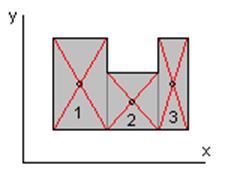
Некоторые тела сложной формы можно разбить на
части, положение центра масс которых известно или может быть предварительно
определено. Тогда используем общие формулы, только вместо элементарных частиц
тела берутся конечные части, на которые оно разбито.
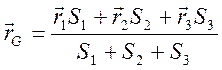
б) метод отрицательных масс
В тех случаях, когда фигуру, положение центра
масс которой мы хотим определить, можно дополнить до фигуры, положение центра
масс которой хорошо известно, можно использовать метод «отрицательных» масс. В
примере прямоугольник с вырезом представляется в виде разности большого (1) и
малого (2) прямоугольников. Используем прежние формулы с условием, что масса
вырезаемой части считается отрицательной. Этот метод особенно удобен при
вычислении положения центров масс тел, имеющих отверстия. Для тел сложной формы
можно использовать комбинацию методов а) и б).
в) теорема Гюльдена №1
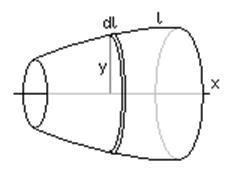Рассмотрим кривую l.
Приведем ее во вращение вокруг оси х. Получим тело вращения. Элемент кривой dl при этом образует кольцо, площадь которого dS мы запишем и, проинтегрировав по всей кривой, получим
выражение для площади боковой поверхности тела вращения:
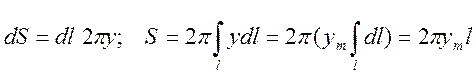
т.к.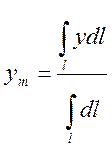 
Формулировка теоремы Гюльдена №1 у нас получается следующей:
Площадь боковой поверхности тела вращения равна произведению длины окружности, описанной центром масс образующей (2pym), на длину линии l, т.е. S=2pym l.
Эта теорема может быть полезна в тех случаях, когда нам хорошо известна боковая площадь поверхности тела вращения и длина кривой, ее образующей.
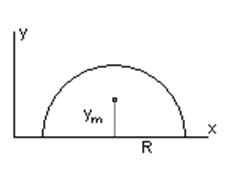
В качестве примера рассмотрим
полуокружность радиуса R. Приведем ее во вращение
вокруг оси х и получим сферу. Площадь поверхности сферы - 4pR2. Длина
полуокружности - pR,
Обозначим положение центра масс полуокружности через ym,
отсюда имеем 4pR2
= 2pym pR. В итоге получаем: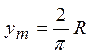 
.
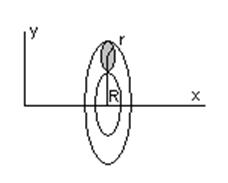В качестве другого примера получим хорошо известную из
геометрии формулу для боковой поверхности тора.
Рассмотрим на плоскости xy окружность радиуса r, ее центр находится на расстоянии R от оси x. Приведем ее во вращение вокруг оси и получим тор. Площадь его боковой поверхности будет равна:
Sбок = 2pym 2pr = 2pR 2pr = 4p2Rr.
г) теорема Гюльдена №2
Рассмотрим на плоскости xy плоскую фигуру площадью S.
Выделим в ней элемент площади dS, его координата
– y. Приведем фигуру во вращение вокруг оси x. Элемент dS образует
тор, объем которого будет равен dV = dS 2py. Проинтегрируем и найдем объем тела вращения, которое у
нас при этом получится.
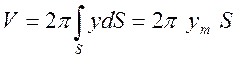, т.к.
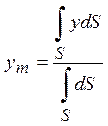, а выражение в знаменателе есть площадь
фигуры S.
Формулировка теоремы Гюльдена №2 у нас получается следующей:
Объем тела вращения равен произведению длины окружности, описанной центром масс сечения (2pym), на площадь сечения S, то есть V=2pym S.
Эта теорема может быть полезна в тех случаях, когда нам хорошо известен объем тела вращения и площадь фигуры, его образующей.
В качестве примера применения теоремы Гюльдена №2 рассмотрим полудиск.
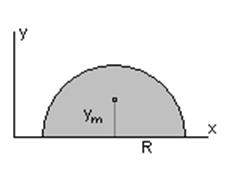
Расположим полудиск радиуса R как показано на рисунке. Приведем полудиск во вращение вокруг оси x и получим сферу. По теореме объем сферы равен: (4/3)pR3 = 2pym (pR2/2) и отсюда
ym = (4/3p)R.
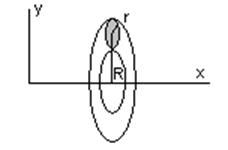Другим примером будет получение известной из
геометрии формулы для объема тора, который получается при приведении во
вращение вокруг оси x окружности радиуса r, центр которой расположен на расстоянии R от оси x.
V = 2pym pr2 = 2pR pr2 = 2p2Rr2
Для некоторых простых фигур и тел приведем результаты без вывода (часто они понятны даже с точки зрения здравого смысла).
1. Центр масс однородного прямолинейного отрезка лежит в середине отрезка.
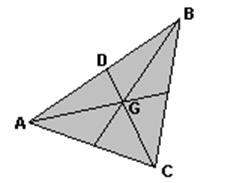
2. Центр масс треугольника лежит в точке пересечения медиан. Медианы в точке пересечения делят друг друга в отношении 2:1 (CG=2 GD)
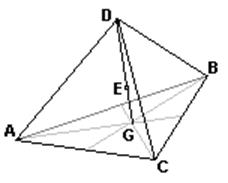
3. Для пирамиды центр масс Е лежит на прямой, проведенной из вершины D в центр масс основания G. Точка Е делит отрезок DG в отношении 1:3 (DE=3EG). Этот результат справедлив для любой пирамиды и, как предельный случай, для конуса. При этом точка D не обязательно должна находиться над точкой G (то есть пирамида не обязательно должна быть прямой).
В тех случаях, когда форма фигуры или тела, положение центра масс которых необходимо определить, являются достаточно сложными, можно применить метод прямого интегрирования. При этом используем интегральные определения, приведенные в начале параграфа.
Рассмотрим дугу окружности радиуса R с углом раствора 2a0.
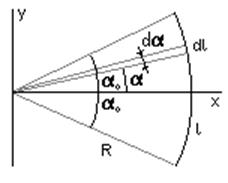Выделим бесконечно малый элемент дуги dl
с углом раствора da и текущим углом a.
Длина этого элемента равна dl = Rda, его координата x=RCosa.. Определим положение центра масс дуги по
оси x:
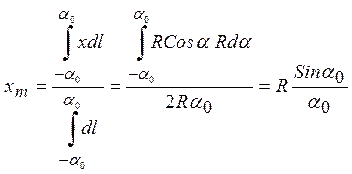
Этот результат при a0=p/2 дает нам формулу для полуокружности, полученную ранее.
Рассмотрим круговой сектор радиуса R с углом раствора 2a0. Расположим его симметрично оси x, как показано на рисунке. Выделим бесконечно малый сектор с углом раствора da и текущим углом a. В пределе бесконечно малых он представляет собой треугольник высотой R и основанием dl=Rda. Площадь этого треугольника равна dS = (1/2)R2da. Центр масс треугольника лежит в точке пересечения медиан. Таким образом, в проекции на ось x координата положения центра масс треугольника имеет значение x = (2/3)RCosa. Используя определение положения центра масс по оси x, будем иметь для всего сектора:
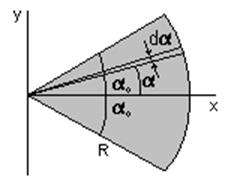
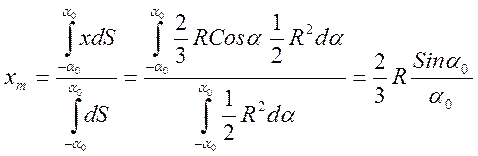
Легко видеть, что для полудиска (a0=p/2) мы получим формулу, которая была ранее выведена с помощью теоремы Гюльдена №2.
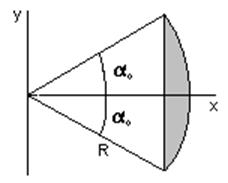В качестве последнего примера определения
положения центра масс фигур рассмотрим круговой сегмент радиуса R и углом раствора 2a0. Его можно рассматривать как «разность» кругового
сектора и треугольника. Тогда, используя формулы для треугольника и сектора, а
также метод отрицательных масс, можно для кругового сегмента получить формулу
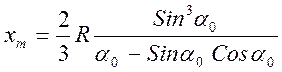
Эта формула при a0=p/2 также даст ранее полученную формулу для полудиска.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.