








13.1. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ.
ОСНОВНАЯ ТРИГОНОМЕТРИЧЕСКАЯ СИСТЕМА ФУНКЦИЙ (ОТС)
Пусть
на [a,b] заданы
функции f(x) и ![]() , такие, что
, такие, что ![]() -
интегрируемая на [a,b]
функция. Функции f(x)
и
-
интегрируемая на [a,b]
функция. Функции f(x)
и ![]() называются ортогональными на [a,b], если
называются ортогональными на [a,b], если 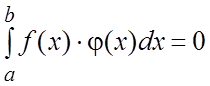 .
.
Бесконечная система функций
![]() (1.1)
(1.1)
называется ортогональной
на [a,b], если ![]()
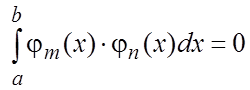 и
и 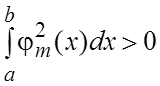 эти функции попарно ортогональны на [a,b].
эти функции попарно ортогональны на [a,b].
Примеры ортогональных систем:
а) Основная тригонометрическая система (ОТС):
1, cosx, sinx, cos2x, sin2x,…, cosnx, sinnx,… (1.2)
ортогональна на ![]() .
.
б) Система функций:
sinx, sin2x,…, sinnx,… (1.3)
ортогональна на ![]() .
.
в) Тригонометрическая система (ТС):
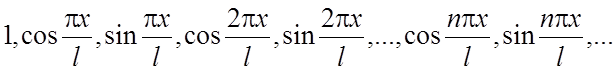 (1.4)
(1.4)
ортогональна
на ![]() .
.
13.2. РЯД ФУРЬЕ ПО ОРТОГОНАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ
Пусть задана произвольная, ортогональная на [a,b] система функций (1.1).
Ряд
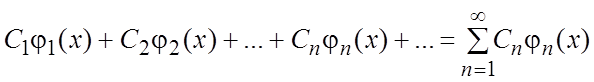 (2.1)
(2.1)
называется рядом Фурье для функции f(x) по системе (1.1), если
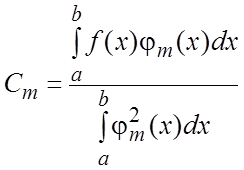 (2.2)
(2.2)
![]() , вычисленные по формуле (2.2) называются коэффициентами
Фурье.
, вычисленные по формуле (2.2) называются коэффициентами
Фурье.
13.3. ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
а) Ряд Фурье по ТС (1.4)
Теорема 1. (Дирихле). Если ![]() -
периодическая функция с Т = 2l, кусочно-гладкая
на
-
периодическая функция с Т = 2l, кусочно-гладкая
на ![]() (на этом интервале f(x) и
(на этом интервале f(x) и ![]() имеют не более
конечного числа точек разрыва, притом лишь первого рода), то
тригонометрический ряд Фурье по ТС (1.4) для f(x)
имеют не более
конечного числа точек разрыва, притом лишь первого рода), то
тригонометрический ряд Фурье по ТС (1.4) для f(x)
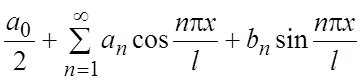 , (3.1)
, (3.1)
где
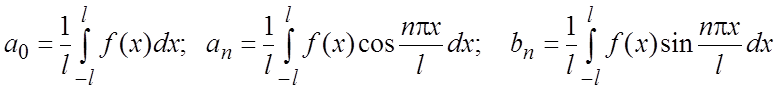 , n=1,2,3…(3.2)
, n=1,2,3…(3.2)
сходится к f(x), если x – точка непрерывности f(x) и к 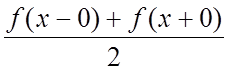 , если x – точка разрыва f(x), где
, если x – точка разрыва f(x), где ![]() и
и ![]() - соответственно левый и правый пределы f(x) в точке x:
- соответственно левый и правый пределы f(x) в точке x:
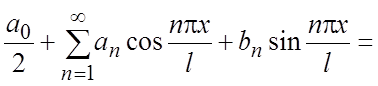
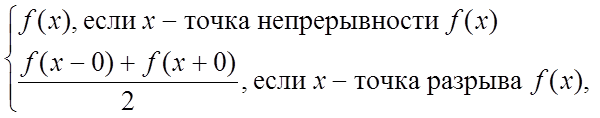
![]() - называются коэффициентами Фурье.
- называются коэффициентами Фурье.
Функция
![]() , совпадающая с
, совпадающая с ![]() в
в ![]() и удовлетворяющая условию
и удовлетворяющая условию ![]() , называется периодическим продолжением
, называется периодическим продолжением
![]() на всю ось Ox.
на всю ось Ox.
В ряд
Фурье можно разложить и непериодическую кусочно-гладкую функцию, заданную лишь
в интервале ![]() , вычисляя коэффициенты
, вычисляя коэффициенты ![]() по формулам (3.2). Полученный ряд будет
сходиться на всей числовой оси, а его суммой будет
по формулам (3.2). Полученный ряд будет
сходиться на всей числовой оси, а его суммой будет ![]() -
периодическое продолжение
-
периодическое продолжение ![]() на ось Ox.
на ось Ox.
При
вычислении коэффициентов Фурье в формулах (3.2) интервал интегрирования ![]() можно заменить любым интервалом
можно заменить любым интервалом ![]() длины 2l.
длины 2l.
б) Неполные ряды Фурье.
Если ![]() - четная функция, то
- четная функция, то
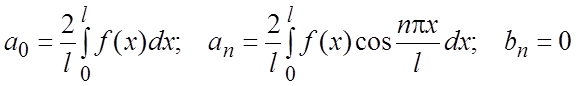 . (3.3)
. (3.3)
Ряд Фурье примет
вид: 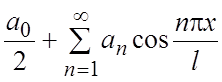 .
.
Если ![]() - нечетная функция, то
- нечетная функция, то 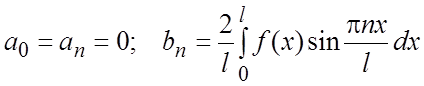 (3.4)
(3.4)
и ряд Фурье принимает
вид 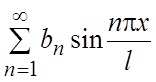 .
.
в) Функцию ![]() , кусочно –гладкую в интервале
, кусочно –гладкую в интервале ![]() , можно разложить в ряд Фурье только по
косинусам или по синусам. Для этого достаточно продолжить
, можно разложить в ряд Фурье только по
косинусам или по синусам. Для этого достаточно продолжить ![]() четным или соответственно нечетным образом
на интервал
четным или соответственно нечетным образом
на интервал ![]() и для полученной на
и для полученной на ![]() функции составить ряд Фурье. Коэффициенты
Фурье будут при этом вычисляться по формулам соответственно (3.3) или (3.4).
функции составить ряд Фурье. Коэффициенты
Фурье будут при этом вычисляться по формулам соответственно (3.3) или (3.4).
г) Комплексная
форма тригонометрического ряда Фурье для ![]() ,
периодической с Т = 2l, а также для
,
периодической с Т = 2l, а также для ![]() , заданной на
, заданной на ![]() имеет
вид
имеет
вид
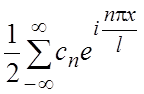 ,
, 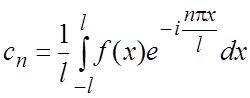 .
.
Связь между ![]() и
и ![]() следующая:
следующая:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
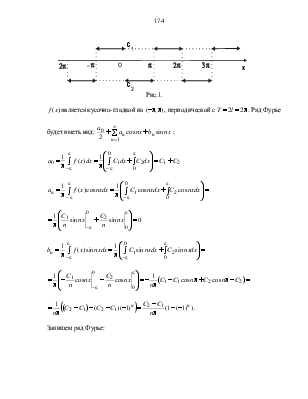
Пример. Разложить в ряд Фурье периодическую (с периодом ![]() ) функцию
) функцию ![]() ,
определенную равенствами:
,
определенную равенствами: 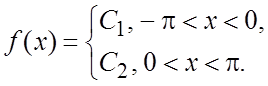
Ñ Начертим график заданной функции:
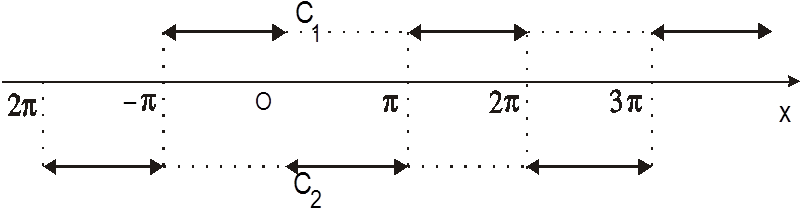 |
![]() является
кусочно-гладкой на
является
кусочно-гладкой на ![]() , периодической с
, периодической с ![]() . Ряд Фурье будет иметь вид:
. Ряд Фурье будет иметь вид: 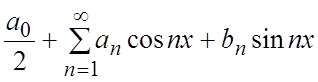 ;
; 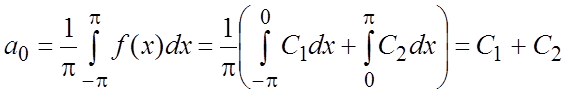
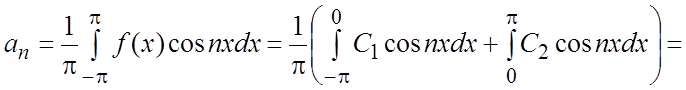
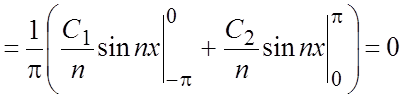
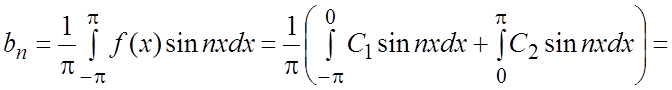
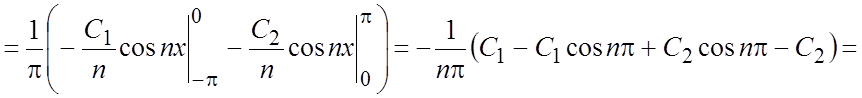
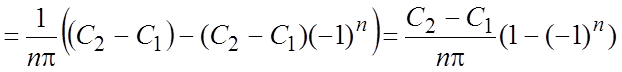 .
.
Запишем ряд Фурье:
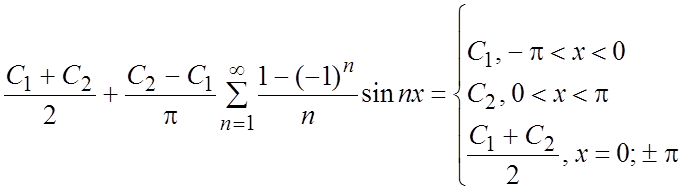
(сумма ряда
записана в соответствии с теоремой 1: в точках непрерывности ![]() ряд Фурье сходится к
ряд Фурье сходится к ![]() , а в точках разрыва
, а в точках разрыва ![]() - к среднему арифметическому односторонних
пределов
- к среднему арифметическому односторонних
пределов ![]() в этих точках).#
в этих точках).#
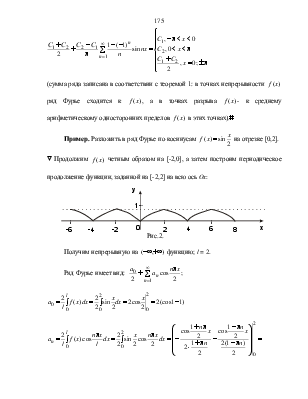
Пример. Разложить в ряд Фурье по косинусам 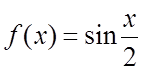 на
отрезке [0,2].
на
отрезке [0,2].
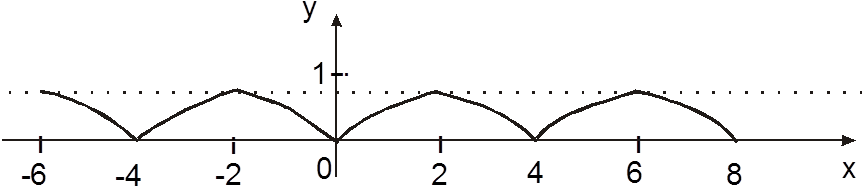 |
Рис.2.
Получим непрерывную на ![]() функцию; l = 2.
функцию; l = 2.
Ряд Фурье имеет вид: 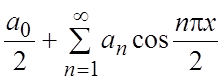 ;
;
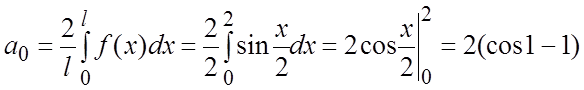
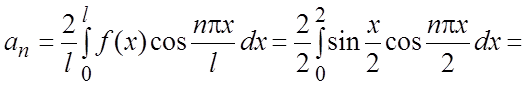
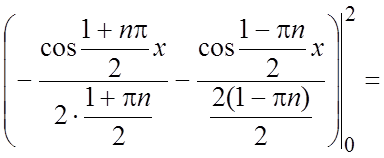
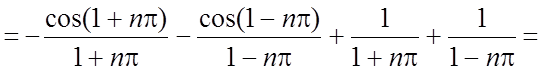
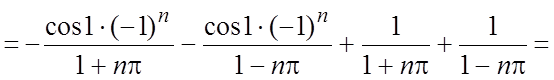
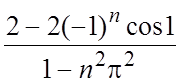 .
.
Ряд Фурье: 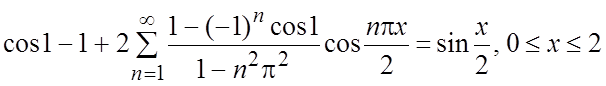 #
#
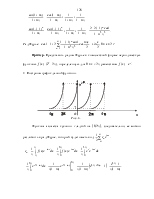
Пример. Представить рядом Фурье в комплексной форме периодическую
функцию ![]()
![]() , определенную для
, определенную для ![]() равенством
равенством ![]() .
.
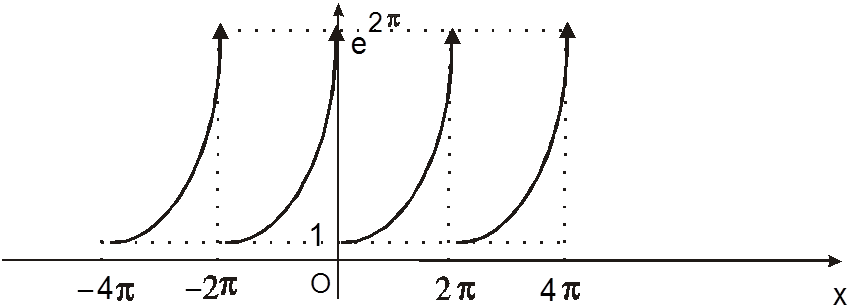 |
Рис. 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.