Распространение быстрых заряженных частиц через вещество, страница 2

Для оценки тормозной способности ионов можно воспользоваться общей формулой (@) для ионизационных потерь частицей, приняв . Тогда получим (в Ландау, с.721 торможение на одном атоме)

,

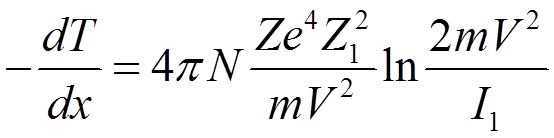где  - заряд рассеивающей частицы.

 

Видно, что легкие и тяжелые частицы при одинаковой скорости теряют энергию на единице пути одинаково.

 

При одинаковой энергии частиц потери тяжелой частицы резко возрастают:

.

 

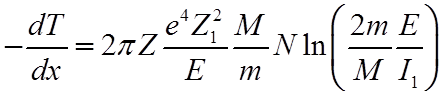распространении релятивистских частиц. Оценка ионизационных потерь

Постановка задачи

Пусть частица с зарядом 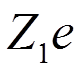 пролетает вдоль оси xсо скоростью V

 на расстоянии   от электрона атома, который рассматривается, как свободный.

Предполагаем, что скорость частицы остается постоянной: 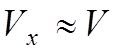. Основное возмущение направлено перпендикулярно , что приводит к формированию перпендикулярного импульса

,

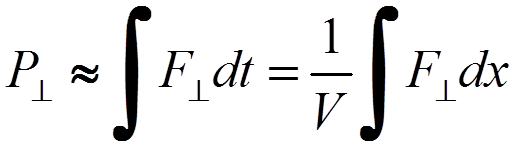  где   .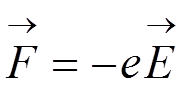

 

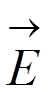Для вычисления  применим теорему Гаусса, рассматривая бесконечный цилиндр радиуса , в центре которого при x = 0 находится заряд .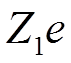

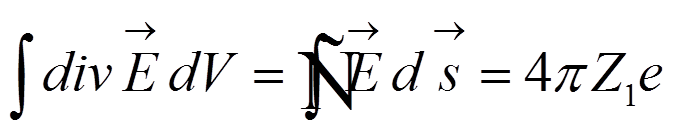
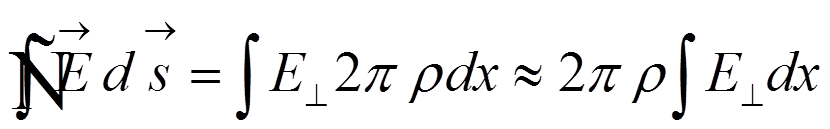Учитывая, что         , получим

.

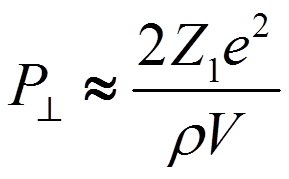Что дает оценку величины переданной энергии

.

 

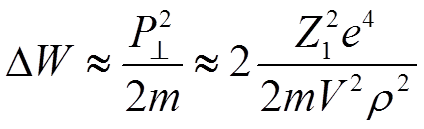Потери энергии

В указанном приближении потери энергии можно представить в виде

.

 

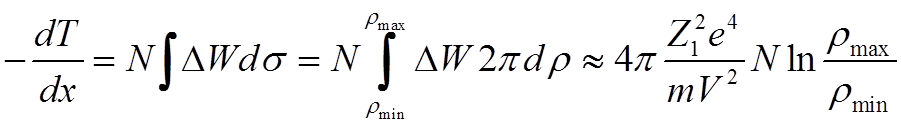Определим пределы интегрирования 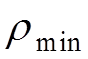 и .

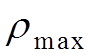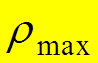
За время взаимодействия   электрон в атоме должен оставаться неподвижным, т.е.  .  Классическая частота вращения электрона в атоме порядка частоты излучаемого атомом фотона, т.е.  . Тогда 

.

В релятивистском случае распределение поля зависит от скорости.

С увеличением V поле оказывается локализовано в области , где  ,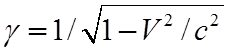

что приводит к уменьшению времени взаимодействия  .

 .

 

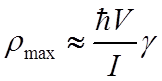Учитывая, что , получаем

.

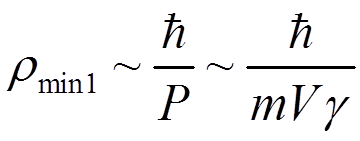m - масса рассеянного электрона .

Для оценки  необходимо также учитывать, что электрону не может передана скорость более 2V, т.е.  

.

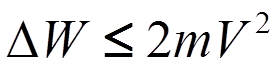В нерелятивистском случае получим

.

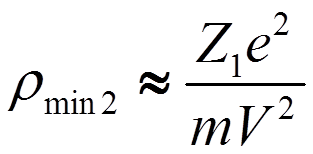В релятивистском случае, приравнивая переданный импульс   к  , получим

 .

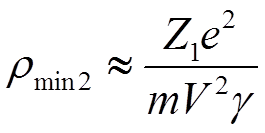Очевидно, что  определяется из условия

.

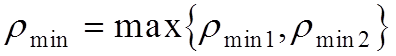Учитывая, что

,

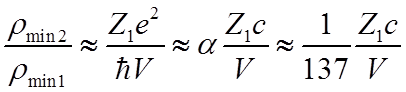видим, что при    определяется квантовыми эффектами.

Окончательно получим формулу для потерь

.

 

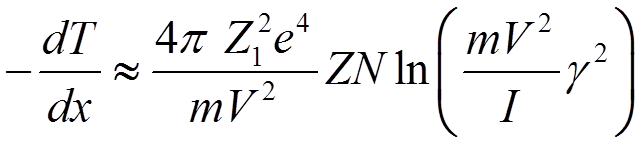Для электронов (Z₁ = 1) в ультрарелятивистском случае можно получить формулу

.

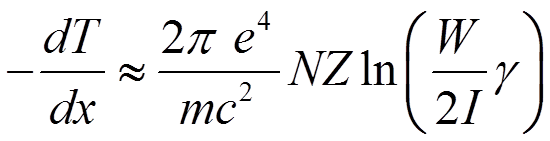Следовательно, при большой энергии  потери возрастают .

 

Сравним потери электронов и протонов.

в нерелятивистском случае:

·  при одинаковых скоростях   .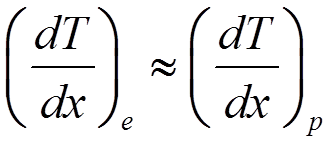

·  при одинаковых энергиях потери протонов в  раз больше.

 

в релятивистском случае:

при V ~ c  потери определяются величиной ln  и практически не зависят от массы: 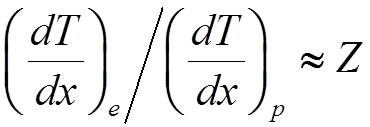        (при W = 1 Гэв).

 

Радиационные потери энергии

при движении электронов в веществе

 

Заряженная частица при столкновении с атомом в результате торможения излучает электромагнитную волну.

Интенсивность тормозного излучения

,

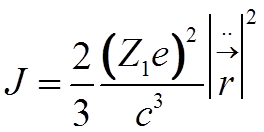где 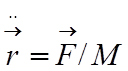 - ускорение частицы с зарядом Ze . Видно, что в одинаковом поле  при 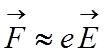  излучение пропорционально M^-2 , т.е. тяжелые частицы не имеют радиационных потерь.