Другой пример: частица вращается на ниточке по окружности
радиуса ![]() с постоянной скоростью
с постоянной скоростью ![]() . Работа не совершается т.к. сила натяжения
ниточки перпендикулярна скорости. А кинетическая энергия в системе отсчета,
движущейся равномерно со скоростью
. Работа не совершается т.к. сила натяжения
ниточки перпендикулярна скорости. А кинетическая энергия в системе отсчета,
движущейся равномерно со скоростью ![]() меняется от 0 до
меняется от 0 до ![]() . Как это объяснить?
. Как это объяснить?
Получим закон преобразования кинетической
энергии системы частиц при переходе из одной инерциальной системы отсчета в
другую. Пусть имеется неподвижная система отсчета ![]() и
движущаяся со скоростью
и
движущаяся со скоростью ![]() система
система ![]() . Для любой
. Для любой ![]() -ой
частицы
-ой
частицы ![]() . Полный импульс частиц в системе
. Полный импульс частиц в системе ![]() -
-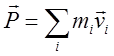 ,
соответственно в системе
,
соответственно в системе ![]() -
- 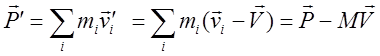 , где
, где ![]() -
полная масса системы частиц.
-
полная масса системы частиц.
Преобразуем энергию:
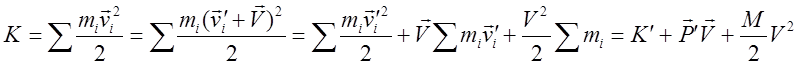 . (8)
. (8)
Перейдем в систему отсчета в которой центр масс покоится. В
этой системе ![]() т.к.
т.к. ![]() . Отсюда
(8) примет вид:
. Отсюда
(8) примет вид:
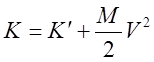 (9)
(9)
Равенство (9) выражает собой теорему Кенига: кинетическая энергия системы частиц в лабораторной системе отсчета равна сумме кинетических энергий системы в системе центра масс и кинетической энергии относительного поступательного сдвига полной массы системы со скоростью центра масс.
Потенциальная энергия.
Рассмотрим работу, совершаемую при перемещении
частицы в некотором силовом поле ![]() . Простой пример
силового поля представляет собой однородное поле тяжести, котором действующая
сила:
. Простой пример
силового поля представляет собой однородное поле тяжести, котором действующая
сила: ![]() . Допустим, что наряду с силовым полем
. Допустим, что наряду с силовым полем ![]() действует также внешняя сила
действует также внешняя сила ![]() . Для простоты рассмотрим одномерный
случай, в котором
. Для простоты рассмотрим одномерный
случай, в котором ![]() и
и ![]() направлены
вдоль одной оси. Согласно (4):
направлены
вдоль одной оси. Согласно (4):
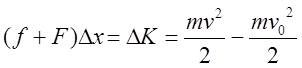 ,
,
или
![]() . (10)
. (10)
Можно подобрать внешнюю силу такой, чтобы ![]() . Ясно, что в этом случае
. Ясно, что в этом случае ![]() .
.
Возникает вопрос – куда идет работа внешней силы?
Определим потенциальную энергию таким образом, чтобы ее
изменение ![]() , тогда работа внешней силы
, тогда работа внешней силы ![]() равна таким образом определенному
изменению потенциальной энергии
равна таким образом определенному
изменению потенциальной энергии ![]() . Потенциальная энергия
определяется изменением положения частицы в силовом поле. В общем случае
. Потенциальная энергия
определяется изменением положения частицы в силовом поле. В общем случае ![]() работа при бесконечно малом перемещении
работа при бесконечно малом перемещении ![]() , в случае конечного пути –
, в случае конечного пути –
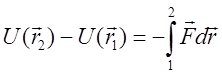 . (11)
. (11)
Подчеркнем, что в выражении (11) существенен знак минус.
Силовые поля ![]() , в которых значение интеграла (11) не
зависит от пути перемещения, называются консервативными или потенциальными.
В противном случае определение потенциальной энергии теряет смысл. Другим
равносильным определению о независимости интеграла от пути консервативности
силы является равенство нулю работы по замкнутому контуру. Действительно, интеграл
по замкнутому контуру в поле консервативных сил
, в которых значение интеграла (11) не
зависит от пути перемещения, называются консервативными или потенциальными.
В противном случае определение потенциальной энергии теряет смысл. Другим
равносильным определению о независимости интеграла от пути консервативности
силы является равенство нулю работы по замкнутому контуру. Действительно, интеграл
по замкнутому контуру в поле консервативных сил ![]() ,
поскольку значения потенциальной энергии на концах контура совпадают т.е.
,
поскольку значения потенциальной энергии на концах контура совпадают т.е.![]() . (см. рис n2)
. (см. рис n2)
Примеры. Потенциальная энергия деформации пружины. При
изменении длины пружины на ![]() возникает сила
упругости пропорциональная удлинению
возникает сила
упругости пропорциональная удлинению ![]() . Изменение
потенциальной энергии:
. Изменение
потенциальной энергии:
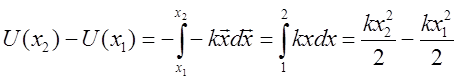 . Потенциальная энергия
определена с точностью до константы, т.к. измеряется всегда только изменение
потенциальной энергии. В приложении к потенциальной энергии упругой деформации
удобно считать
. Потенциальная энергия
определена с точностью до константы, т.к. измеряется всегда только изменение
потенциальной энергии. В приложении к потенциальной энергии упругой деформации
удобно считать ![]() . Тогда
. Тогда 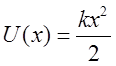 ,
x – удлинение.
,
x – удлинение.
Потенциальная энергия в поле тяготения. Гравитационное поле называется центральным, поскольку сила тяготения действует в направлении радиус – вектора, соединяющего взаимодействующие тела. При произвольном выборе начала отсчета системы (см. рис n3):
![]() . Учитывая, что
. Учитывая, что ![]() , поскольку сила действует по линии соединяющей
тяготеющие тела, получаем:
, поскольку сила действует по линии соединяющей
тяготеющие тела, получаем: ![]()
Сила, действующая со стороны тяготеющего центра массы ![]() на частицу массы
на частицу массы ![]() ,
помещенную в поле:
,
помещенную в поле: 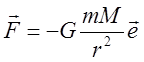 . Изменение потенциальной энергии
между точкам, отстоящими от центра на расстояния
. Изменение потенциальной энергии
между точкам, отстоящими от центра на расстояния ![]()
![]() :
:
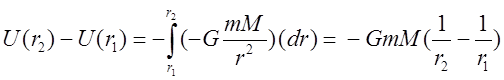 (12)
(12)
Удобно считать потенциальную энергию на больших расстояниях стремящейся к нулю:
![]() , при такой калибровке-
, при такой калибровке-
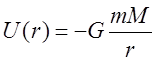 (13)
(13)
Соотношение между силой и потенциальной энергией
Для одномерного движения непосредственно из определения (11) следует выражение силы через потенциальную энергию:
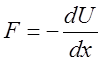 (14)
(14)
В общем случае, когда известна функция ![]() определим убыль потенциальной энергии как
работу силы при бесконечно малом перемещении
определим убыль потенциальной энергии как
работу силы при бесконечно малом перемещении![]() .
Расписывая скалярное произведение покомпонентно, имеем:
.
Расписывая скалярное произведение покомпонентно, имеем:
![]() . Применяя правила вычисления
полного дифференциала функции многих переменных, находим:
. Применяя правила вычисления
полного дифференциала функции многих переменных, находим: 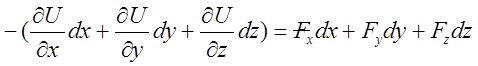 . Сравнивая коэффициенты при одинаковых
приращениях координат, получаем:
. Сравнивая коэффициенты при одинаковых
приращениях координат, получаем:
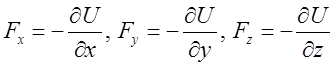 (15)
(15)
Формулы (15) записываются в векторном виде как:
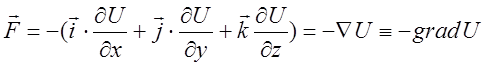 (16)
(16)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.