






Внешними
силами материальной системы называются силы, с которыми действуют на точки
системы тела и точки, не входящие в рассматриваемую систему, будем их
обозначать 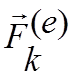 .
.
Внутренними силами материальной системы называют силы
взаимодействия между точками рассматриваемой системы, мы их будем обозначать 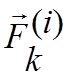 .
.
Внутренние и внешние силы могут включать в себя как активные силы, так и реакции связей.
 Пусть
система состоит из n точек. Тогда по третьему закону Ньютона, например для
точек 1 и 2, внутренние силы взаимодействия этих точек равны по величине и
противоположны по направлению:
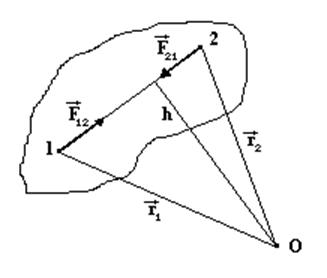
Пусть
система состоит из n точек. Тогда по третьему закону Ньютона, например для
точек 1 и 2, внутренние силы взаимодействия этих точек равны по величине и
противоположны по направлению: 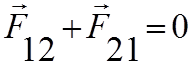
Равнодействующая внутренних сил состоит из векторной суммы сил действия и противодействия, которая равна нулю:
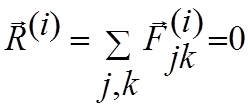 .
.
Если
рассмотреть сумму моментов сил 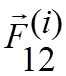 и
и 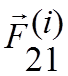 относительно некоторой произвольной точки
О, то легко видеть, что
относительно некоторой произвольной точки
О, то легко видеть, что
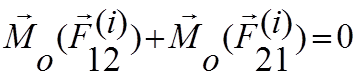
т.к. обе силы имеют одинаковые плечи h и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы этих моментов внутренних сил:
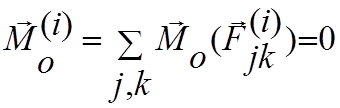
§3.5 Дифференциальные уравнения движения системы
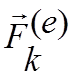 и равнодействующую силу всех внутренних
сил
и равнодействующую силу всех внутренних
сил 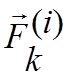 , то для любой к-ой точки системы
можно составить дифференциальное уравнение движения в виде второго закона
Ньютона:
, то для любой к-ой точки системы
можно составить дифференциальное уравнение движения в виде второго закона
Ньютона: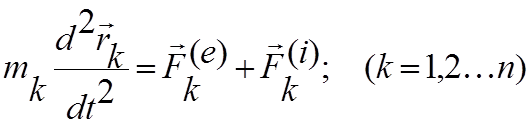
Систему этих уравнений называют дифференциальными уравнениями движения механической системы в векторной форме. Если спроектировать их на оси координат, то получим 3n скалярных дифференциальных уравнения.
Мы видели, с какими трудностями приходится сталкиваться при интегрировании дифференциального уравнения движения точки, если сила зависит от времени, положения или скорости. Здесь же мы имеем систему уравнений и трудности неизмеримо возрастают. Поэтому особую роль в динамике системы материальных точек играют общие теоремы, позволяющие в отдельных случаях получить информацию о характере движения системы без выполнения трудоемкого интегрирования системы дифференциальных уравнений.
§3.6 Геометрические характеристики системы материальных точек. Моменты инерции. Теорема Штейнера. Эллипсоид инерции.
|
|
Рассмотрим точку О, прямую L и плоскость В, а также точки материальной системы (одна из них Ai с массой mi). Расстояния от точки Ai до точки О, прямой L и плоскости В обозначим через ri, Di и di соответственно. |
Можно составить выражения:
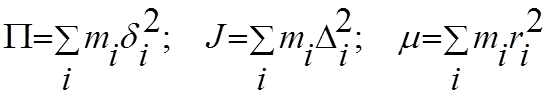
Суммирование распространено по всем точкам материальной системы. Эти выражения называются моментами инерции соответственно относительно плоскости В, прямой L и точки О.
Аналитические выражения моментов инерции относительно основных координатных элементов связаны равенствами:
Jz=Pxz+Pzy, m=Pzx+Pzy+Pxy
(Момент инерции относительно какой-либо оси равен сумме моментов инерции относительно двух ортогональных плоскостей, проходящих через эту ось. Момент инерции относительно точки равен сумме моментов инерции относительно трех ортогональных плоскостей, пересекающихся в этой точке.)
Для сплошных тел суммы перейдут в интегралы:
|
Пример 1.
|
Для
шара массы m, радиуса R (плотность
(поскольку |
|
|
Проведем через центр масс материальной системы с координатами a,b,c оси x’,y’,z’ параллельно осям x,y,z. Тогда для любой точки системы xi=xi’+a, yi=yi’+b и момент инерции системы относительно оси z равен |
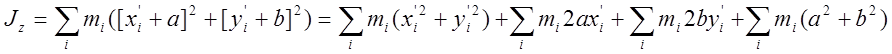
Второе
и третье слагаемое равны нулю в силу того, что в системе отсчета, связанной с
центром масс, 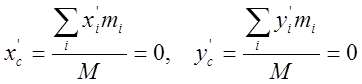 , а в четвертом слагаемом a2+b2=d2 (d – расстояние между осями z и z’).
Первое слагаемое есть момент инерции системы относительно оси z’.
Окончательно имеем:
, а в четвертом слагаемом a2+b2=d2 (d – расстояние между осями z и z’).
Первое слагаемое есть момент инерции системы относительно оси z’.
Окончательно имеем:
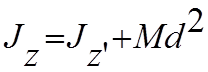 ,
,
то есть момент инерции относительно какой-либо оси z равен моменту инерции относительно параллельной и проходящей через центр масс оси z’ плюс Md2, где d – расстояние между осями.
Следствие: Среди параллельных осей та проходит через центр масс, для которой момент инерции имеет наименьшее значение.
Аналогичное утверждение справедливо для плоскостей (моментов P).
Пример 2.
|
|
Рассмотрим однородный цилиндр массы M, радиуса R и высотой, равной 1. Записав
момент инерции цилиндрического слоя радиуса r и толщиной dr
относительно оси z0 и
проинтегрировав от 0 до R получим: |
по теореме Штейнера момент инерции цилиндра относительно
оси z’ равен 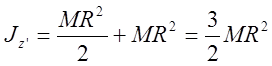
Пример 3.
|
|
Поместим начало оси x, направленной влево, в правом конце стержня массы M и длины l. Записав момент инерции произвольного элемента dx, находящегося на расстоянии x от оси z’ (лежит в плоскости рисунка) и проинтегрировав по длине стержня получим: |
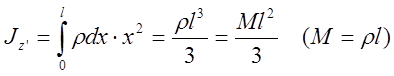
по теореме Штейнера момент инерции стержня
относительно оси z0 равен 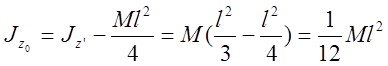
Пример 4. Определим
момент инерции однородного эллипсоида с полуосями a,b,c
относительно оси x, проходящей через центр эллипсоида. Эту задачу сведем
к решенной ранее в этом параграфе задаче о моментах инерции однородного шара,
используя тот факт, что преобразование x=ax’, y=by’, z=cz’
преобразует эллипсоид 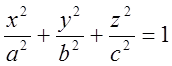 в шар единичного радиуса.
в шар единичного радиуса.
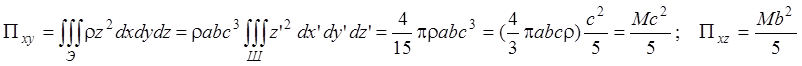
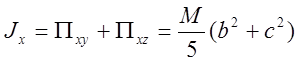
|
|
Рассмотрим систему точек mi с координатами xi,yi,zi. Возьмем луч, проходящий через точку О и имеющий направляющие косинусы a, b, g. Di – расстояние i-ой точки до луча:
или
|
Отсюда момент инерции Jматериальной системы относительно луча (a,b,g) равен:
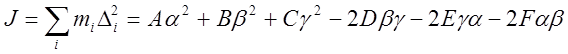 (3.6.1),
(3.6.1),
где 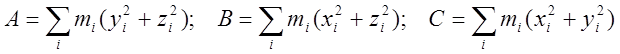
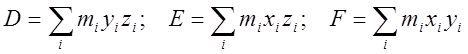
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.