Простейшие свойства внутренних сил системы. Дифференциальные уравнения движения системы, страница 2

            A,B,C обозначают моменты инерции системы относительно осей координат, D,E и F – произведения инерции или центробежные моменты инерции относительно тех же осей.

            На луче строим точку Р по формуле 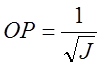, ее координатами будут величины

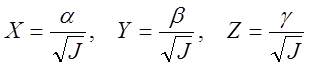
            Уравнение геометрического места точек Р отсюда в силу (3.6.1) будет

            Если материальная система представляет собой объемное тело, то поверхность этого геометрического места точек представляет собой эллипсоид. Этот эллипсоид называется эллипсоидом инерции системы, построенным относительно точки О. Эллипсоид инерции рассматриваемой системы изменяется при изменении точки, относительно которой он строился. Центральным эллипсоидом инерции называется эллипсоид инерции, построенный относительно центра масс рассматриваемой материальной системы или тела. Главные оси эллипсоида инерции называются главными осями инерции тела относительно точки О.

Замечание. Если D=0 и E=0, то ось z является главной осью эллипсоида инерции.

Не всякий эллипсоид может являться эллипсоидом инерции, ибо для эллипсоида инерции должно выполняться условие: A+B>C; B+C>A; C+A>B.

Общие теоремы динамики системы

§3.7 Теоремы об изменении количества движения и о движении центра масс

Количество движения точки и системы

   Количеством  движения материальной точки  называют вектор, равный произведению массы точки на ее скорость, т.е.

     Количество движения точки в физике часто называют импульсом материальной точки. Проекции количества движения точки на декартовы оси координат    

     Количеством движения системы  называют векторную сумму количеств движения отдельных точек системы, т.е.

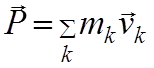
Вектор количества движения системы в отличие от вектора количества движения точки не имеет точки приложения. Вектор количества движения точки считается приложенным к самой движущейся точке, а вектор количества движения системы является свободным вектором.

     Количество движения системы можно выразить через массу системы и скорость центра масс

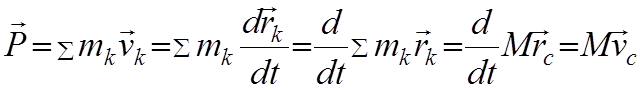
если масса системы не изменяется при движении.

Элементарный и полный импульс силы

     Действие силы  на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным импульсом силы . Полный импульс силы за время t  определяют по формуле

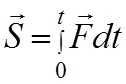
Теорема об изменении количества движения точки

Дифференциальное уравнение движения материальной точки под действием силы  можно представить в следующей векторной форме:

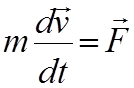
     Так как масса точки считается постоянной, то ее можно внести под знак производной. Тогда

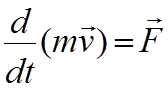
     Эта формула выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе. (Причиной изменения количества движения точки является сила).

     В проекциях на оси координат теорема записывается следующим образом:

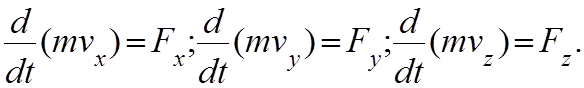
    Если обе части теоремы умножить на dt, то получим другую форму этой же теоремы

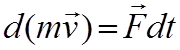
т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.

     Интегрируя обе части в пределах от нуля до t, имеем:

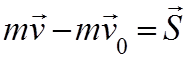
где -скорость точки в момент t, -скорость при t=0, -импульс силы за время t.

     Это выражение часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.

Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.

Теорема об изменении количества движения системы

            Для каждой точки системы, находящейся под действием внешних и внутренних сил, имеем:

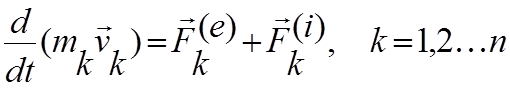
            Проведя суммирование по всем точкам системы получим:

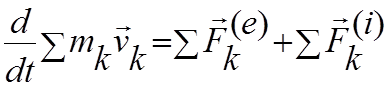
используя свойства внутренних сил системы и определение количества движения системы 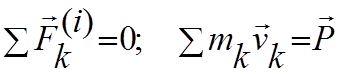  окончательно имеем:

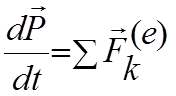
            Теорема об изменении количества движения системы: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему.

            В другой форме теорема выглядит так:

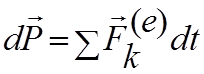
            Дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему.

            Теорема импульсов в конечной (интегральной) форме:

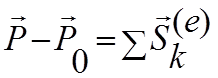
            Изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время.

            В проекциях на оси координат

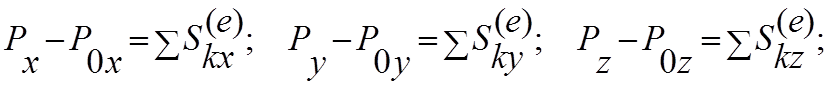
            Видно, что внутренние силы не входят в теорему и не влияют на изменение количества движения системы.

Законы сохранения количества движения

            Эти законы представляют собой частные случаи теоремы об изменении количества движения системы.

Если 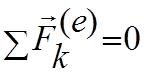   то 

т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.

            Если равна нулю проекция главного вектора внешних сил только на одну ось системы координат, то имеем P_x=const, т.е. проекция количества движения системы на ту же ось является постоянной величиной (сохраняется).

Если мы имеем тело, разрывающееся под действием внутренних сил на две части, то полный импульс системы, состоящей из двух частей, сохраняется, т.е.

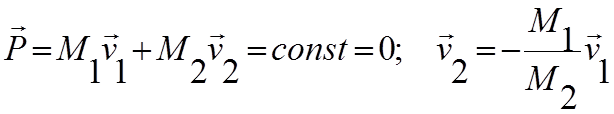
Теорема о движении центра масс

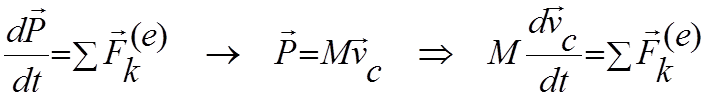или

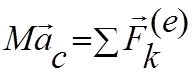
т.е. центр масс системы движется как точка по второму закону Ньютона, как если бы к ней была приложена равнодействующая всех внешних сил.

            Следствие:  Если главный вектор внешних сил, действующих на систему, равен нулю, то ускорение центра масс равно нулю, а, следовательно, скорость центра масс является постоянной по модулю и направлению. Имеем, что центр масс движется прямолинейно и равномерно по инерции или находится в покое.