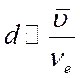Плазма. Основные понятия. Классификация плазмы, страница 3

          ,                                                                                                   (1.20)

где  ─ средняя скорость теплового движения. Полагая 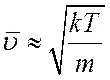 из выражения (1.20) получаем

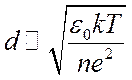          .                                                                                           (1.21)

Экранированный кулоновский потенциал

          Предположим, что мы поместили в плазму точечный заряд , где  - зарядовое число и нас интересует стационарное распределение зарядов, которое устанавливается около него. В непосредственной близости к заряду  (рис. 1.1) плотность отрицательных зарядов будет превышать плотность положительных и этот избыток постепенно уменьшается по мере увеличения 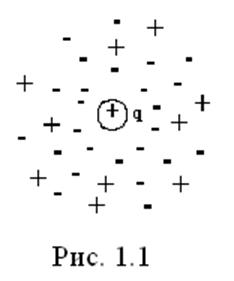расстояния  от заряда . Такое распределение возникает вследствие того, что  одновременно притягивает отрицательные заряды и отталкивает положительные. На достаточно больших расстояниях  от заряда  плазма возвращается в состояние макроскопической квазинейтральности. В результате перераспределения зарядов плазмы вдали от заряда возникают электрические поля, которые полностью компенсируют электрическое поле, создаваемое зарядом .

          Связь между плотностью суммарного заряда  и электростатическим потенциалом  определяется уравнением Пуассона

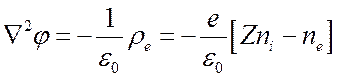          ,                                                              (1.22)

где  и  плотность ионов и электронов. Поскольку плазма вблизи заряда  находится в состоянии термодинамического равновесия, то плотности зарядов есть     

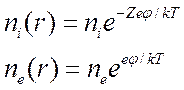,                                                                                    (1.23)

где  и  плотности соответствующих величин на значительном расстоянии от заряда  и плазма там квазинейтральна. Тогда из закона сохранения заряда следует .  

С учетом выражений (1.23) уравнение (1.22) в сферической системе координат запишется

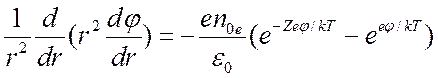          .                                                (1.24)

Для идеальной плазмы согласно выражению (1.2)  и, разлагая экспоненты в ряд,  уравнение (1.24) запишется

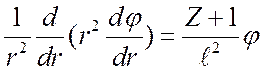,                                                                        (1.25)

где

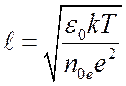                                                                                              (1.26)

Введением безразмерной координаты  уравнение (1.25) приводится к виду

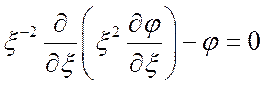                                                                                    (1.27)

решение, которого есть , где  - постоянная интегрирования, или

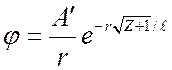          .                                                                                      (1.28)

Для определения постоянной  воспользуемся тем, что при  . Поэтому в окрестности заряда

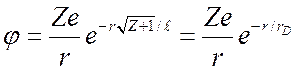          ,                                                                    (1.29)

где

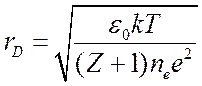                                                                                            (1.30а) называется длиной экранирования или дебаевским радиусом. Сравнивая выражения (1.21) и (1.30) видим, что радиус Дебая и является пространственным масштабом разделения зарядов.

В единицах СИ

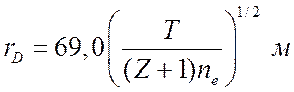          .                                                                    (1.30б)