Двухатомная
молекула (N = 2) имеет одну внутреннюю степень свободы (2×3-5=1) и обладает, следовательно, одним
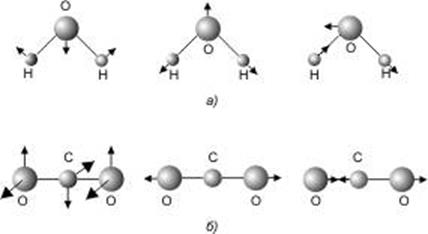
нормальным колебанием. Молекула воды (![]() )
обладает 3N - 6 = 3
нормальными колебаниями (см. рис. 27). Мода 1 является симметричным изгибным
колебанием, 2 — симметричным растяжением и сжатием, 3 — асимметричным
колебанием деформаций. Молекула
)
обладает 3N - 6 = 3
нормальными колебаниями (см. рис. 27). Мода 1 является симметричным изгибным
колебанием, 2 — симметричным растяжением и сжатием, 3 — асимметричным
колебанием деформаций. Молекула ![]() является линейной и
обладает 3N - 5 = 4
модами колебаний. Две моды 1 (рис. 27б) являются изгибными колебаниями в
двух взаимно перпендикулярных направлениях, имеющими одинаковые энергии. Мода 2
— симметричное и 3 — асимметричное колебание.
является линейной и
обладает 3N - 5 = 4
модами колебаний. Две моды 1 (рис. 27б) являются изгибными колебаниями в
двух взаимно перпендикулярных направлениях, имеющими одинаковые энергии. Мода 2
— симметричное и 3 — асимметричное колебание.
В сложной
многоатомной молекуле могут существовать нормальные колебания, в которых группы
атомов движутся как целое, а их относительное движение внутри группы
несущественно. Такие группы имеют характерную частоту колебаний. Например,
группа ОН имеет характерную частоту ![]() ,
, ![]() —
—
![]() Гц. Характерные частоты колебаний зависят,
естественно, от характера связей между атомами группы и связей с другими
атомами молекулы.
Гц. Характерные частоты колебаний зависят,
естественно, от характера связей между атомами группы и связей с другими
атомами молекулы.
|

|

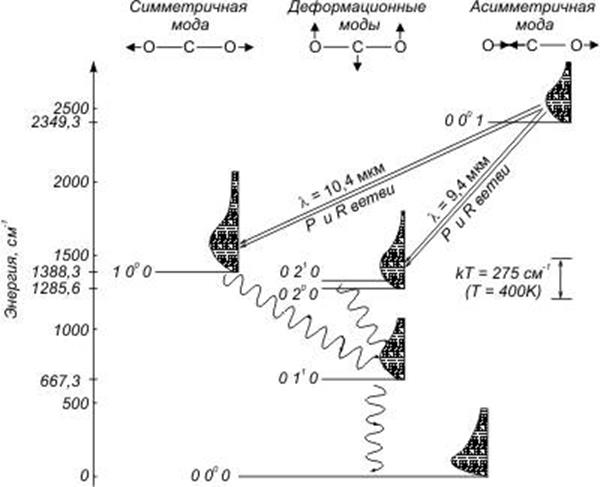
![]() имеет частоту
имеет частоту ![]() Гц
Гц
![]()
![]() Гц
Гц
![]()
![]() Гц.
Гц.
Остается учесть вращательное движение. Усредняя оператор энергии (110) как по электронным, так и по колебательным движениям
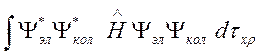 ,
,
мы получим
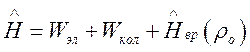 , (117)
, (117)
где использовано предположение о медленности вращения по сравнению с колебаниями.
Гамильтониан 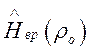 аналогичен (98), только моменты инерции записаны
для равновесной конфигурации, то есть при
аналогичен (98), только моменты инерции записаны
для равновесной конфигурации, то есть при ![]() .
.
Нахождение
собственных значений энергии вращающегося тела (волчка) наиболее просто для
случая, когда все три главных момента энергии тела одинаковы ![]() (шаровой волчок). Гамильтониан (98)
принимает вид
(шаровой волчок). Гамильтониан (98)
принимает вид
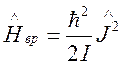 ,
(118)
,
(118)
и его собственные значения равны 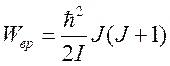 . Каждый уровень вырожден (2J + 1)
раз по направлениям момента относительно самого тела. Волновые функции
симметричного волчка, в основном, совпадают (при изменении обозначения
квантовых чисел) с угловой частью волновой функции двухатомной молекулы. Если
описать вращение с помощью эйлеровых углов
. Каждый уровень вырожден (2J + 1)
раз по направлениям момента относительно самого тела. Волновые функции
симметричного волчка, в основном, совпадают (при изменении обозначения
квантовых чисел) с угловой частью волновой функции двухатомной молекулы. Если
описать вращение с помощью эйлеровых углов ![]() то получим [1]
то получим [1]
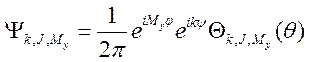 ,
,
где ![]() —
вычислена в [1, § 82]. При
—
вычислена в [1, § 82]. При ![]() (симметричный
волчок) имеем
(симметричный
волчок) имеем
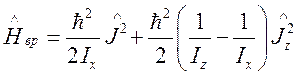 (119)
(119)
и
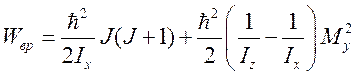 . (120)
. (120)
Уровни энергии только двухкратно
вырождены при данном J и ![]() по направлению проекции
момента.
по направлению проекции
момента.
При ![]() (асимметричный волчок) вычисление
уровней энергии в общем виде невозможно. Вырождение снимается полностью. Имеем
2J + 1 уровней энергии.
(асимметричный волчок) вычисление
уровней энергии в общем виде невозможно. Вырождение снимается полностью. Имеем
2J + 1 уровней энергии.
Мы приведем здесь лишь результат расчета W [1]
J = 1 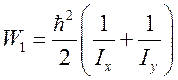 ;
;
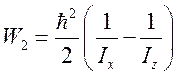 ;
;
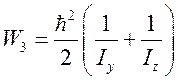 .
.
J = 2 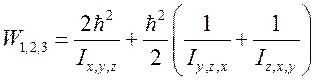 ;
;
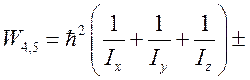
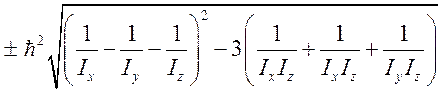 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.