Левый годограф
– годограф заведомо устойчивой системы, не охватывает точки ![]() , что и требуется согласно критерию
Найквиста для устойчивости замкнутой системы. Правый годограф – годограф трёхполюсной,
заведомо неустойчивой системы обходит точку
, что и требуется согласно критерию
Найквиста для устойчивости замкнутой системы. Правый годограф – годограф трёхполюсной,
заведомо неустойчивой системы обходит точку ![]() три
раза против часовой стрелки, что и требуется согласно критерию Найквиста
для устойчивости замкнутой системы.
три
раза против часовой стрелки, что и требуется согласно критерию Найквиста
для устойчивости замкнутой системы.
Замечание.
Амплитудно-фазовые
характеристики систем с действительными параметрами – а только такие и
встречаются на практике, симметричны относительно действительной оси. Поэтому
обычно рассматривается только половина амплитудно-фазовой характеристики,
соответствующая положительным частотам. При этом считаются полуобходы точки ![]() . Пересечение отрезка (
. Пересечение отрезка (![]() ) при увеличении частоты сверху вниз (фаза
растёт) считается за
) при увеличении частоты сверху вниз (фаза
растёт) считается за ![]() пересечение, а снизу вверх – за
пересечение, а снизу вверх – за ![]() пересечение. Если амплитудно-фазовая
характеристика разомкнутой системы начинается на отрезке (
пересечение. Если амплитудно-фазовая
характеристика разомкнутой системы начинается на отрезке (![]() ), то этому будет соответствовать
), то этому будет соответствовать ![]() или
или ![]() пересечение
в зависимости от того, вниз или вверх идёт характеристика при возрастании
частоты.
пересечение
в зависимости от того, вниз или вверх идёт характеристика при возрастании
частоты.
Подсчёт числа
пересечений отрезка (![]() ) можно произвести по логарифмическим
частотным характеристикам. Уточним, это те пересечения, которым соответствует
фаза
) можно произвести по логарифмическим
частотным характеристикам. Уточним, это те пересечения, которым соответствует
фаза ![]() при модуле амплитудной характеристики
больше единицы.
при модуле амплитудной характеристики
больше единицы.
Определение устойчивости по логарифмическим частотным характеристикам.
Чтобы воспользоваться критерием Михайлова, надо
построить годограф ![]() . Здесь
. Здесь ![]() –
характеристический полином замкнутой системы.
–
характеристический полином замкнутой системы.
В случае критерия
Найквиста достаточно знать передаточную функцию ![]() разомкнутой
системы. При этом нет необходимости строить годограф. Для определения
устойчивости по Найквисту, достаточно построить логарифмические амплитудную и
фазовую частотные характеристики разомкнутой системы.
разомкнутой
системы. При этом нет необходимости строить годограф. Для определения
устойчивости по Найквисту, достаточно построить логарифмические амплитудную и
фазовую частотные характеристики разомкнутой системы.
Наиболее простое построение получается тогда, когда передаточная функция разомкнутой системы может быть представлена в виде
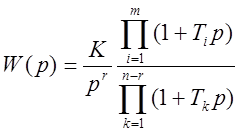 , тогда ЛАХ
, тогда ЛАХ 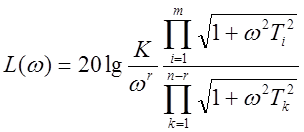 ,
,
ЛФХ  .
.
Рисунок ниже соответствует передаточной функции
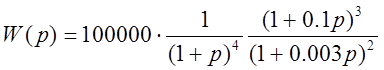 .
.
Здесь ![]() и
и ![]() построены как функции
построены как функции ![]() .
.
Пример.
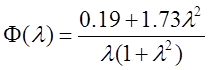 .
.
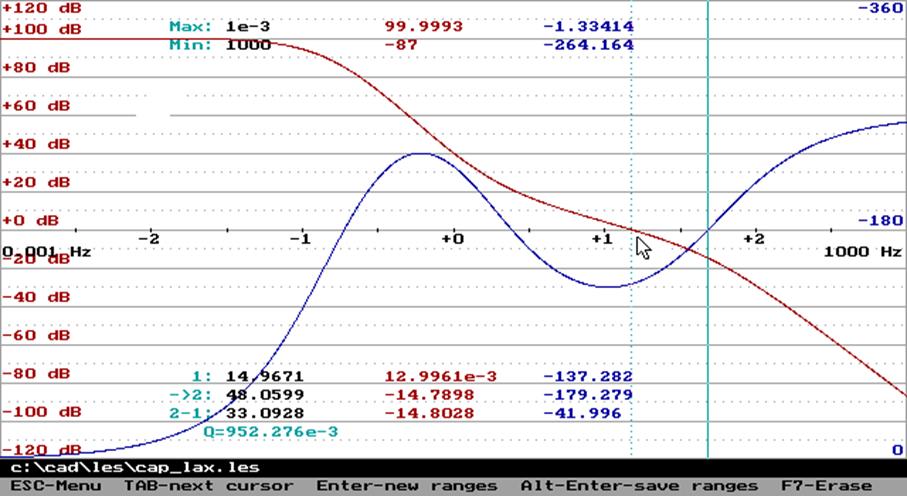
Слева изображены
амплитудная и фазовая частотные характеристики для передаточной функции ![]() , справа – для передаточной функции
, справа – для передаточной функции ![]() , в центре – для исходной передаточной
функции
, в центре – для исходной передаточной
функции ![]() (как это насчитала нам программа Les, метод “Integration”).
(как это насчитала нам программа Les, метод “Integration”).
Три полюса
функции ![]() сдвинуты влево (устойчивая система).
Фазовая характеристика, соответственно, имеет 0 пересечений уровня
сдвинуты влево (устойчивая система).
Фазовая характеристика, соответственно, имеет 0 пересечений уровня ![]() . Три полюса функции
. Три полюса функции ![]() сдвинуты вправо (неустойчивая система).
Фазовая характеристика, соответственно, имеет три полупересечения уровня
сдвинуты вправо (неустойчивая система).
Фазовая характеристика, соответственно, имеет три полупересечения уровня ![]() в областях, где модуль функции передачи
больше единицы.
в областях, где модуль функции передачи
больше единицы.
В любом случае замкнутая система устойчива.
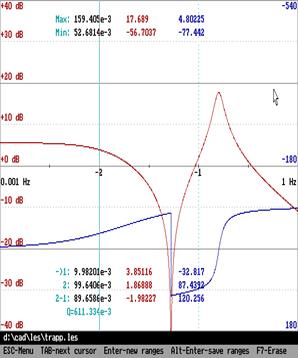
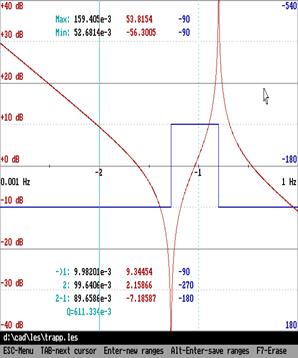
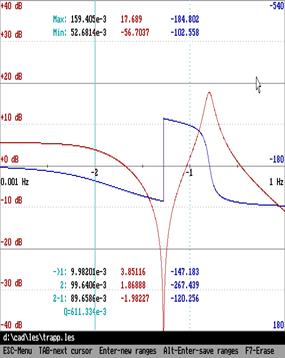
Центральная картинка – расчёт в отсутствие подвижек корней, является предельной для правой картинки, ход фазы на левой картинке радикально отличен. Где истина?
Примеры из [2].
Пусть передаточная функция разомкнутой системы имеет вид:
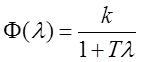 .
.
Разомкнутая
система устойчива при любых положительных k и Т.
Устойчива и замкнутая система, как это видно из годографа ![]() слева на рисунке.
слева на рисунке.
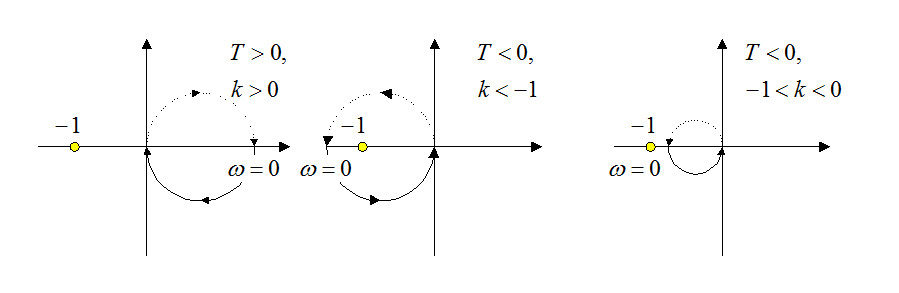
При
отрицательном Т разомкнутая система неустойчива – имеет плюс в правой
полуплоскости. Замкнутая система устойчива при ![]() , как
это видно по годографу в центре, и неустойчива при
, как
это видно по годографу в центре, и неустойчива при ![]() (годограф
справа).
(годограф
справа).
Пусть
передаточная функция разомкнутой системы имеет вид (![]() ):
):
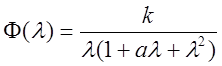 .
.
Она имеет один полюс на мнимой
оси. Следовательно, для устойчивости замкнутой системы необходимо, чтобы число
пересечений амплитудно-фазовой характеристикой разомкнутой системы отрезка (![]() ) действительной оси было равно
) действительной оси было равно ![]() (если рассматривать годограф только для
положительных частот).
(если рассматривать годограф только для
положительных частот).
Как уже упоминалось, автор [2] полагает такую систему неустойчивой.
Согласно
годографу (см. рисунок ниже), при ![]() амплитудно-фазовая
характеристика разомкнутой системы не пересекает отрезок (
амплитудно-фазовая
характеристика разомкнутой системы не пересекает отрезок (![]() ). Зато его пересекает идущая против
часовой стрелки слева полуокружность большого радиуса. Часть этой
полуокружности, соответствующая положительным частотам, начинается на отрезке (
). Зато его пересекает идущая против
часовой стрелки слева полуокружность большого радиуса. Часть этой
полуокружности, соответствующая положительным частотам, начинается на отрезке (![]() ) и идёт вниз от него. Таким образом, имеем
одно полупересечение отрезка (
) и идёт вниз от него. Таким образом, имеем
одно полупересечение отрезка (![]() ), и замкнутая система
будет устойчивой.
), и замкнутая система
будет устойчивой.
Опять-таки, полагая описанную систему устойчивой, построим полуокружность большого радиуса справа. Согласно тому же критерию Найквиста, построенный таким образом годограф соответствует устойчивой замкнутой системе.
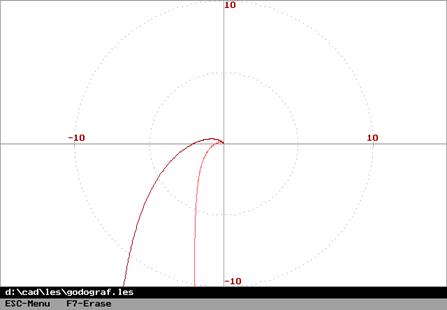
Пусть
передаточная функция разомкнутой системы имеет вид (![]() ):
):
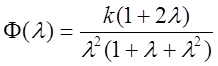 .
.
Она имеет один двойной полюс на
мнимой оси. Следовательно, для устойчивости замкнутой системы требуется одно
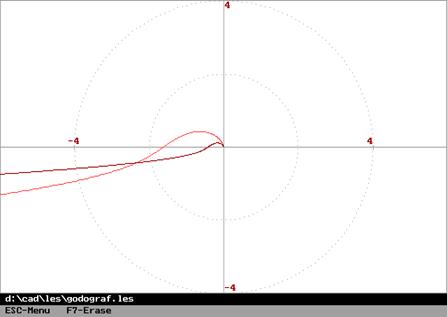
пересечение амплитудно-фазовой характеристикой разомкнутой системы отрезка (![]() ) действительной оси в положительном диапазоне
частот. На рисунке изображены годографы для
) действительной оси в положительном диапазоне
частот. На рисунке изображены годографы для ![]() и
и ![]() . Годограф с
. Годограф с ![]() соответствует
устойчивой в замкнутом состоянии системе.
соответствует
устойчивой в замкнутом состоянии системе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.