§ 2.1. Кинематика точки (неподвижная система координат).
Скорость и ускорение точки в декартовых координатах
Положение точки М0 определяем
радиус-вектором ![]() . Если точка движется
относительно системы отсчета Oxyz, то ее координаты будут функциями времени
. Если точка движется
относительно системы отсчета Oxyz, то ее координаты будут функциями времени
|
|
Скорость и ускорение точки М в некоторый момент времени :
|
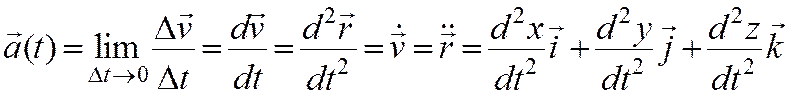
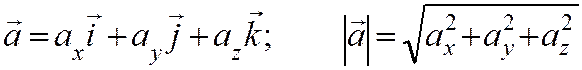
Обозначим через S длину дуги траектории, отсчитываемой с соответствующим знаком от первоначального положения точки на траектории :
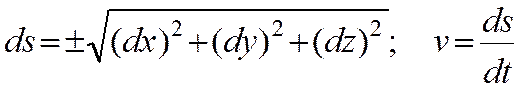
Тогда, очевидно, 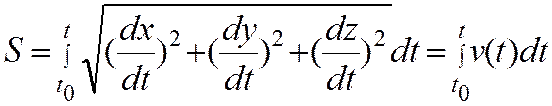
Годограф. К началу неподвижной системы координат О приложим вектор ОР, равный по величине и направлению скорости движущейся точки. При движении точки М по ее траектории точка Р описывает некоторую кривую, называемую годографом скорости точки М. Очевидно, скорость точки годографа Р равна по определению ускорению точки М.
§ 2.2. Скорость и ускорение точки в естественной системе координат
Определим орт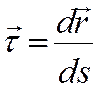 , он
касателен к траектории. Составим отношение
, он
касателен к траектории. Составим отношение 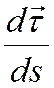 .
Вектор dt ортогонален к орту t, так как
.
Вектор dt ортогонален к орту t, так как ![]()
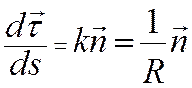 ; где k-кривизна
траектории, R-радиус кривизны траектории.
; где k-кривизна
траектории, R-радиус кривизны траектории.
Третий
орт ![]() определим как
определим как 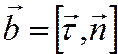
Определим скорость и ускорение точки в естественной системе координат :
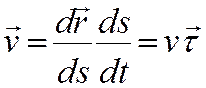 ; т.е.
; т.е. ![]()
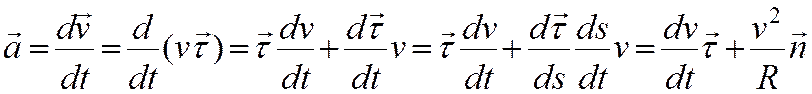
т.е. 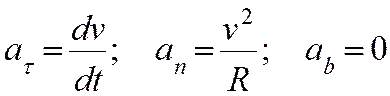
Из последних соотношений получим формулу : 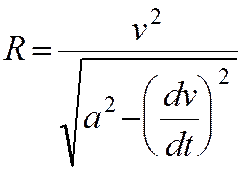
§2. 3. Скорость и ускорение точки в полярных координатах
Положение точки на плоскости известно, если заданы радиус-вектор ![]() и полярный угол
и полярный угол ![]() как
функции времени :
как
функции времени :
|
|
Введем единичный вектор
|
Для производной по времени от единичного вектора имеем :
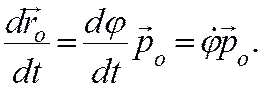
После этого для скорости точки в полярных координатах получаем :
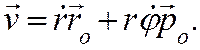
Таким образом радиальная и трансверсальная
составляющие вектора скорости имеют вид : 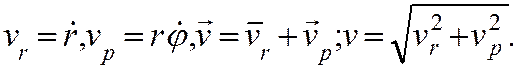
Для ускорения легко получить :
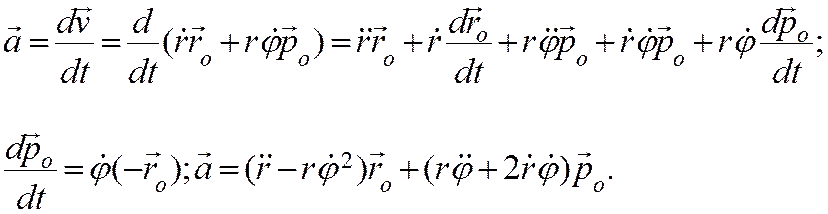
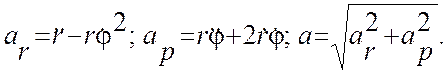
§2. 4. Скорость и ускорение точки в цилиндрических и сферических координатах
Положение точки М в пространстве определяют заданием трех ее цилиндрических координат как функций времени:
|
|
Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат Or, Op, Oz выразится в следующей форме:
|
где
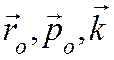 - единичные векторы, направленные по осям
цилиндрической системы координат. Оси Or и Op расположены
в одной плоскости с осями Ox и Oy.
- единичные векторы, направленные по осям
цилиндрической системы координат. Оси Or и Op расположены
в одной плоскости с осями Ox и Oy.
Представим
радиус-вектор ![]() точки М как сумму
двух векторов, т.е.
точки М как сумму
двух векторов, т.е.
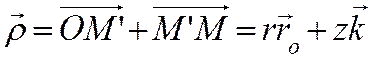
Скорость точки получим дифференцированием радиус-вектора ![]() по времени:
по времени:
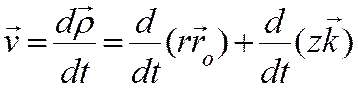
Первое слагаемое в этом выражении вычислялось при выводе скорости точки в
полярных координатах. Во втором слагаемом постоянный по модулю и направлению
единичный вектор ![]() можно вынести за знак
производной. В итоге для скорости получается следующее разложение на
составляющие осям цилиндрической системы координат:
можно вынести за знак
производной. В итоге для скорости получается следующее разложение на
составляющие осям цилиндрической системы координат:
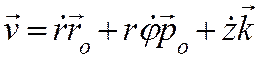
т.е
имеем 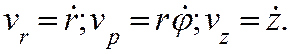 Так как составляющие скорости, параллельные
осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля
скорости имеем:
Так как составляющие скорости, параллельные
осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля
скорости имеем:
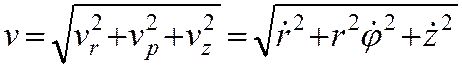
Ускорение точки получим дифференцированием по времени вектора скорости:
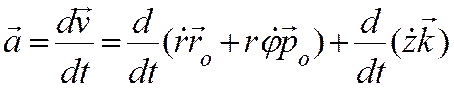
Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах. Во втором слагаемом орт оси z выносим за знак производной. Получим выражение для ускорения точки в составляющих, параллельных осям цилиндрической системы координат:
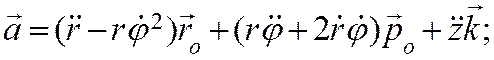
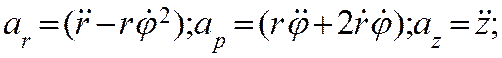
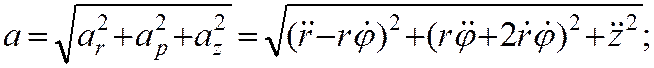
Скорость и ускорение точки в сферических координатах
Сферическими координатами точки М являются величины ![]() . Координатной линией для r
является прямая (r) с базисным ортом
. Координатной линией для r
является прямая (r) с базисным ортом ![]() ,
координатной линией для
,
координатной линией для ![]() служит параллель сферы
с базисным ортом
служит параллель сферы
с базисным ортом ![]() и координатной линией
и координатной линией ![]() - меридиан сферы с базисным ортом
- меридиан сферы с базисным ортом ![]() .
.
Базисные векторы оказались ортогональными. Декартовы координаты x,y,z точки М через сферические выражаются следующими зависимостями :
![]()
Для скорости и ускорения
аналогично цилиндрическим координатам (либо через коэффициенты Ламэ 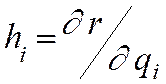 ) можно
получить следующие выражения :
) можно
получить следующие выражения :
|
|
|
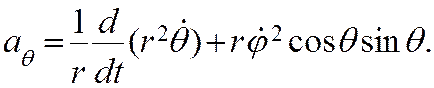
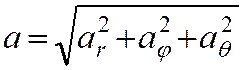
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.