






будет соответствовать
сумма k дробей вида 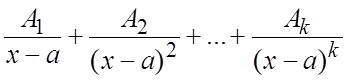 ,
а сомножителю
,
а сомножителю ![]() из (6.4) – сумма дробей
из (6.4) – сумма дробей 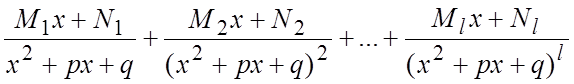 .
.
О нахождении коэффициентов – в разделе 6.8
Пример.
Не определяя коэффициентов, записать разложение правильной дробно-рациональной
функции 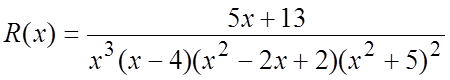 на элементарные дроби.
на элементарные дроби.
Ñ
В разложении знаменателя ![]() на множители
на множители ![]() соответствует действительному корню
соответствует действительному корню ![]() кратности 3,
кратности 3, ![]() – действительному
простому корню
– действительному
простому корню ![]() ,
, ![]() – паре
простых комплексных сопряженных корней
– паре
простых комплексных сопряженных корней ![]() ;
; ![]() – паре комплексных сопряженных корней
– паре комплексных сопряженных корней ![]() кратности 2.
кратности 2.
Тогда разложение ![]() на элементарные дроби будет выглядеть так:
на элементарные дроби будет выглядеть так:
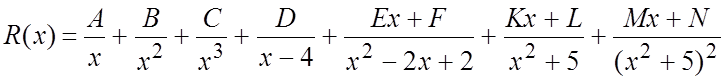 . #
. #
6.7 Интегрирование простейших рациональных дробей
Рассмотрим интегрирование каждой из простейших дробей (6.3).
Дробь I типа.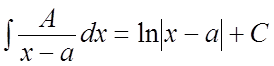 .
.
Дробь II типа. 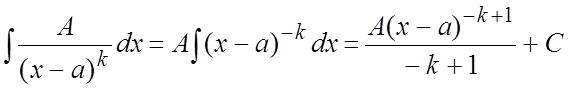 .
.
Дробь III типа. 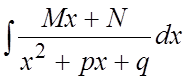 .
.
Создадим в числителе дифференциал
знаменателя, т.е. выражение ![]() .
.
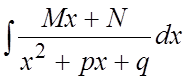 =
=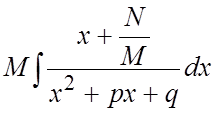 =
=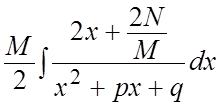 =
=
=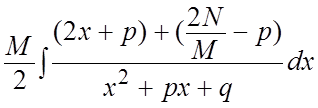 =
=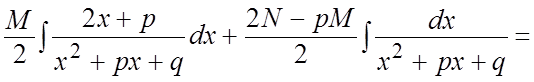
=![]()
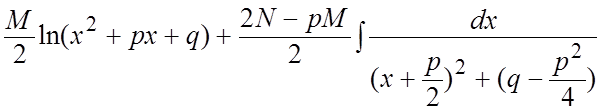 =
=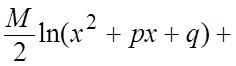
+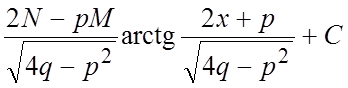 .
.
Дробь IV типа. Интегрирование этих дробей после выделения в числителе
дифференциала квадратного трехчлена ![]() и выделения полного
квадрата в этом трехчлене сводится в вычислению двух интегралов
и выделения полного
квадрата в этом трехчлене сводится в вычислению двух интегралов
1)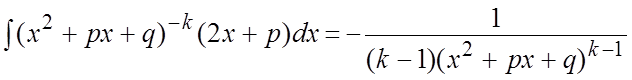 ;
;
2)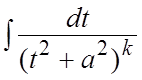 .
(Предварительно сделана замена переменной
.
(Предварительно сделана замена переменной 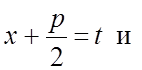
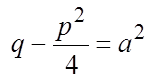 ). Этот интеграл вычисляется по рекуррентной формуле:
). Этот интеграл вычисляется по рекуррентной формуле: 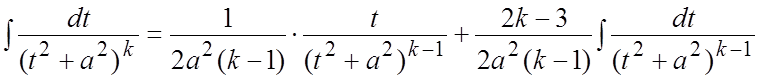 .
.
6.8 Интегрирование рациональных дробей
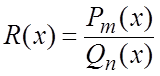 -правильная
рациональная дробь. Чтобы её проинтегрировать, нужно
-правильная
рациональная дробь. Чтобы её проинтегрировать, нужно 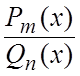 разложить
на сумму элементарных дробей, результат интегрирования которых выражается
элементарными функциями (логарифм, степенная, арктангенс).
разложить
на сумму элементарных дробей, результат интегрирования которых выражается
элементарными функциями (логарифм, степенная, арктангенс).
Если 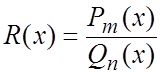 -неправильная рациональная дробь, то деля
числитель на знаменатель, выделяем целую часть, которая является многочленом.
Таким образом,
-неправильная рациональная дробь, то деля
числитель на знаменатель, выделяем целую часть, которая является многочленом.
Таким образом, ![]() можно представить в виде суммы
многочлена и правильной рациональной дроби, об интегрировании которых
говорилось выше.
можно представить в виде суммы
многочлена и правильной рациональной дроби, об интегрировании которых
говорилось выше.
Пример. Найти интеграл  .
.
Ñ Под интегралом стоит правильная
рациональная дробь. Знаменатель её имеет действительные простые корни ![]() . Разложим подынтегральную дробь на
элементарные:
. Разложим подынтегральную дробь на
элементарные:
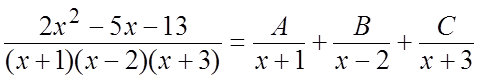 . (8.1)
. (8.1)
Приведя к целому виду обе части этого тождества, получим
![]()
Полагая постепенно![]() , получим систему уравнений
, получим систему уравнений
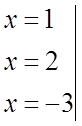
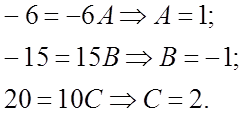
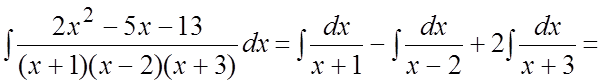
=![]() #
#
Пример. Найти интеграл 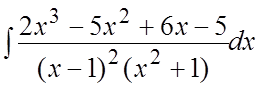 .
.
Ñ Под интегралом – правильная рациональная дробь. Разложение на элементарные дроби имеет вид:
 , (8.2)
, (8.2)
![]() .
.
Коэффициенты![]() можно
найти, приравнивая в этом тождестве коэффициенты при одинаковых степенях
можно
найти, приравнивая в этом тождестве коэффициенты при одинаковых степенях ![]() многочленов, стоящих справа и слева в
(8.2)
многочленов, стоящих справа и слева в
(8.2)
![]()
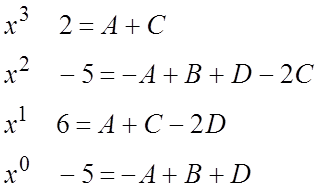
Решив систему уравнений, получим ![]() ,
,
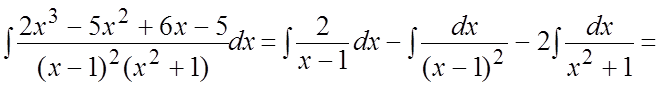
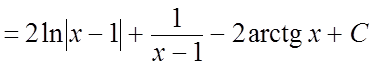 .#
.#
Задачи для самостоятельного решения
72.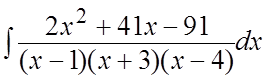 .
73.
.
73.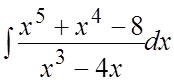 . 74.
. 74.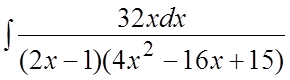 . 75.
. 75.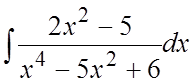 . 76.
. 76.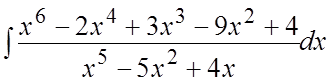 .
77.
.
77. .
.
78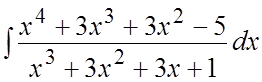 .
79.
.
79.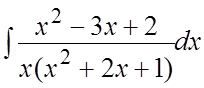 . 80.
. 80.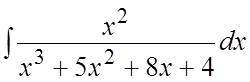 . 81.
. 81.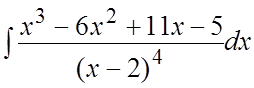 . 82.
. 82.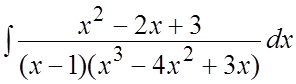 .
83.
.
83.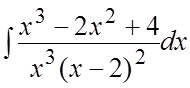 .
.
84.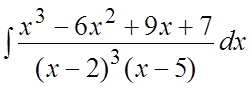 .
85.
.
85.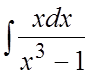 . 86.
. 86. . 87.
. 87.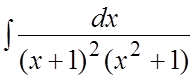 . 88.
. 88.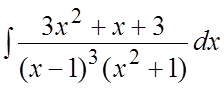 .
89.
.
89.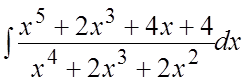 .
.
90.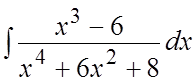 .
91.
.
91.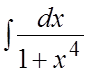 . 92.
. 92.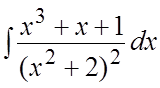 .
93.
.
93.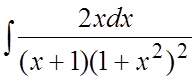 .
.
6.9 Интегрирование некоторых тригонометрических функций.
1) ![]() .
(9.1)
.
(9.1)
Интеграл всегда берется в конечном
виде подстановкой ![]() .
.
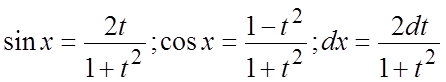 .
.
Эта подстановка является
универсальной для интегралов (9.1). Особенно удобно ею пользоваться, если под
интегралом стоит дробь, в числителе и знаменателе каждой стоят многочлены
относительно ![]() и
и ![]() ,
степени не более первой.
,
степени не более первой.
Пример. Найти интеграл 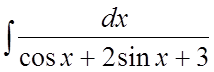 .
.
Ñ Сделаем подстановку 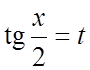 .
. 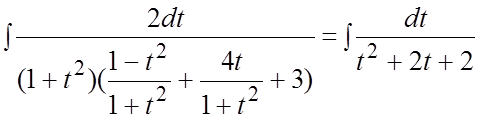 =
=
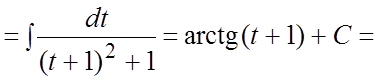
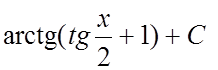 . #
. #
Заметим, что подстановка 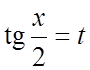 , приводит иной раз к сложным выкладкам.
Ниже указаны случаи, когда цель может быть достигнута с помощью более простых
подстановок.
, приводит иной раз к сложным выкладкам.
Ниже указаны случаи, когда цель может быть достигнута с помощью более простых
подстановок.
2) ![]() .
.
Если имеет место тождество ![]() , то удобнее сделать подстановку
, то удобнее сделать подстановку ![]() ,
, 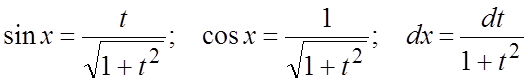 .
.
Пример. Найти интеграл 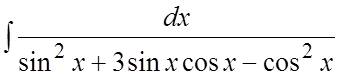 .
.
Ñ Т.к.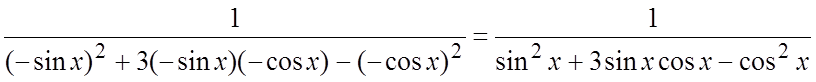 ,
,
то делаем подстановку ![]() , тогда
, тогда 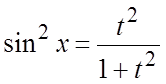 ;
; 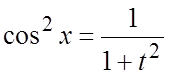 ;
;
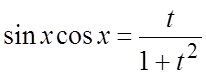 ;
; 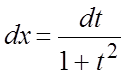 .
. 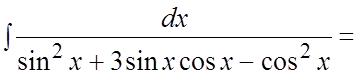
=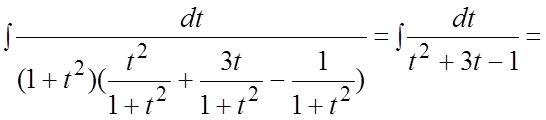
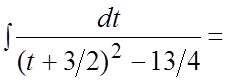
=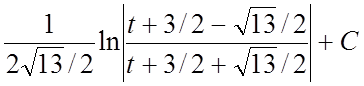
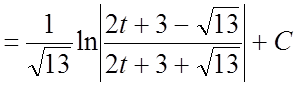 =
=
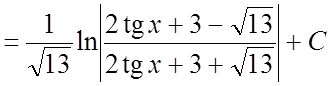 .
.
3)![]() . Для
нахождения этих интегралов применяется подстановка
. Для
нахождения этих интегралов применяется подстановка ![]() .
. ![]() . Подстановка
. Подстановка ![]()
Пример. Найти интеграл 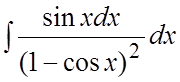
Ñ Сделаем подстановку ![]()
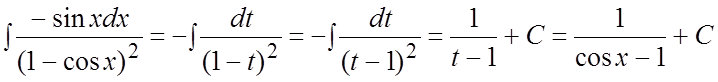 #
#
4) ![]() ,
, ![]()
Интеграл берётся понижением степени ![]() с помощью формул
с помощью формул 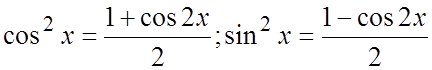 ;
;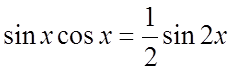
Пример. Найти интеграл![]() .
.
Ñ 
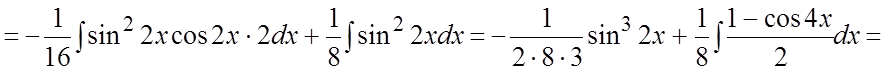
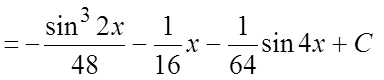 . #
. #
5)![]() .
Хотя бы одно из чисел
.
Хотя бы одно из чисел ![]() – целое положительное нечетное.
Например,
– целое положительное нечетное.
Например, ![]() .
. ![]()
![]()
![]() .
.
Дальше можно сделать подстановку ![]() .
.
Пример. Найти интеграл 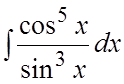 .
.
Ñ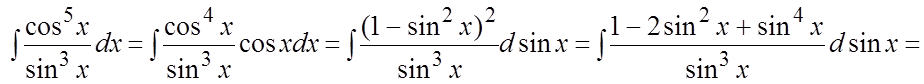
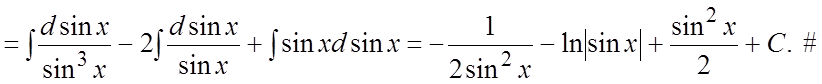
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.