Динамические звенья и их характеристики. Временные характеристики динамических звеньев

Динамические звенья и их характеристики [1].

          Для расчёта различных систем автоматического управления они разбиваются на динамические звенья. Динамическое звено это устройства любого физического вида, описываемое определённым дифференциальным уравнением. Классификация звеньев производится по виду дифференциального уравнения.

          Динамическое звено:

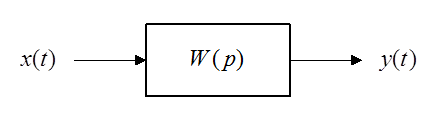
Здесь 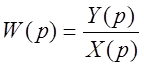 – отношение изображений по Лапласу – передаточная функция.

,  – полиномы от p.

Позиционные динамические звенья.

Безынерционное звено:

, .

Апериодическое звено 1-го порядка:

, .

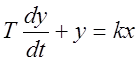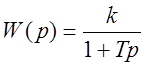Апериодическое звено 2-го порядка:

 (), ,

.

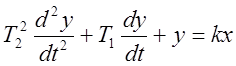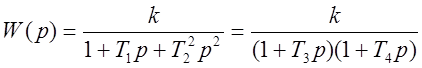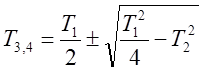Колебательное звено:

 (), .

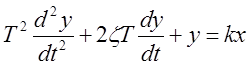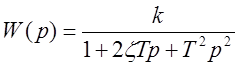Консервативное звено:

, .

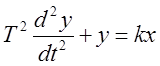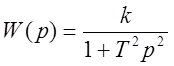Интегрирующие динамические звенья.

Идеальное интегрирующее звено:

 (), .

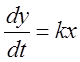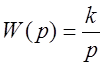Интегрирующее звено с замедлением

, .

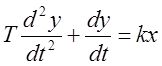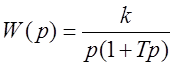Изодромное звено:

, .

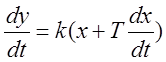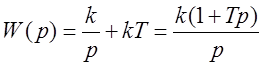Дифференцирующие динамические звенья.

Идеальное дифференцирующее звено:

, .

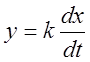Дифференцирующее звено с замедлением:

, .

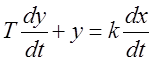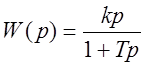Временные характеристики динамических звеньев [1].

Динамические свойства звена определяются по его переходной функции  и функции веса . Функция веса – реакция системы на дельта-функцию.

Переходная же функция звена на его выходе является результатом действия ступенчатой функции  на её входе ( при ). Функция веса является производной по времени от переходной функции: . Доказательство.

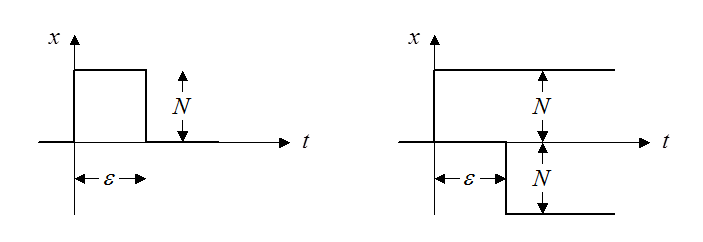
На входе – импульс с площадью . Иначе он может быть представлен двумя ступенчатыми функциями. На выходе:

.

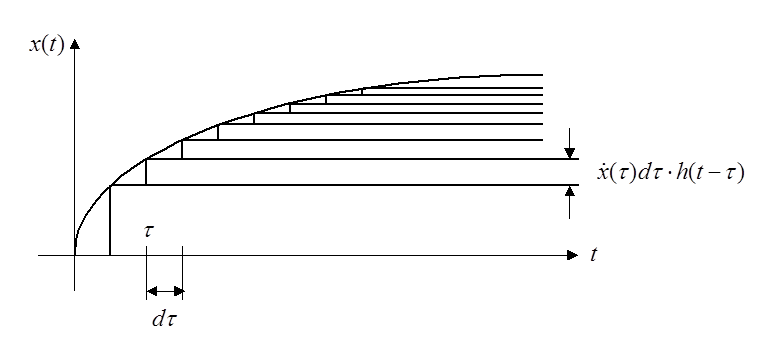
Устремим N к бесконечности, одновременно уменьшая его ширину  так, чтобы площадь импульса оставалась равной единице, т.е. . Получим:

.

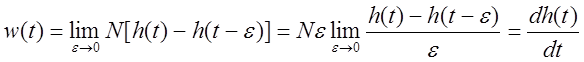Напомним, что функция веса звена связана с его передаточной функцией преобразованием Лапласа – передаточная функция есть изображение функции веса:

.

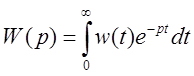          В свою очередь, переходная функция звена связана с его передаточной функцией преобразованием Карстона:

.

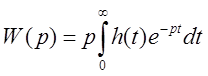Для входного воздействия произвольного вида, переходной процесс на выходе звена при нулевых начальных условиях может быть определён с помощью интеграла Дюамеля-Карстона по переходной функции:

.

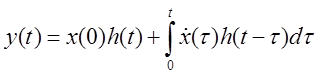или по функции веса:

.

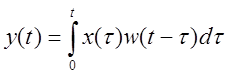Амплитудно-фазовая частотная характеристика.

          Амплитудно-фазовая частотная характеристика (АФХ) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции

при изменении частоты от нуля до бесконечности.

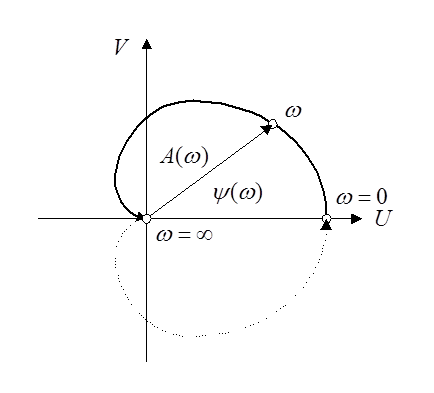
Здесь , ,, .

АФХ строится как для положительных, так и для отрицательных частот. Последняя получается заменой в частотной передаточной функции  на  (получается комплексно сопряжённая величина). Т.е. это зеркальное изображение АФХ для положительных частот относительно вещественной оси.

Смысл отрицательных частот.

Преобразование Фурье (получаемое из преобразования Лапласа подстановкой ):

.

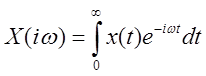Обратное преобразование Фурье:

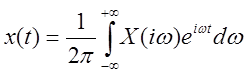
 – бесконечная сумма бесконечно малых по величине векторов, вращающихся на комплексной плоскости с разными угловыми скоростями (частотами) .

            Так как функция времени является вещественной, то каждому элементарному вектору , вращающемуся против часовой стрелки (), должен соответствовать элементарный сопряжённый вектор , вращающийся по часовой стрелке (). В этом случае сумма таких векторов будет всегда вещественной. В принципе можно ограничиться рассмотрением только положительных частот (вопрос удобства).

          Модуль частотной передаточной функции  – чётная функция частоты, фаза  – нечётная функция частоты. Также – чётная функция частоты, а  – нечётная.

Амплитудно-фазовая частотная характеристика и функция веса [2].

          Передаточная функция:

.

Функция веса:

.

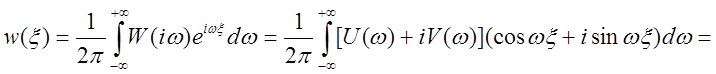
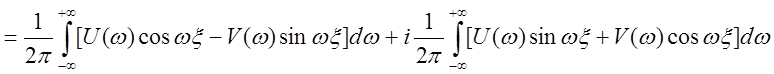Но функция веса – действительная функция. Следовательно:

.

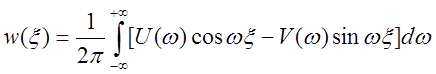Для физически возможных систем  при . Замена  в последнем выражении даёт:

.

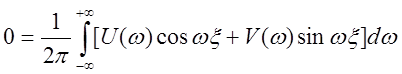Сложением и вычитанием получим ():

, .

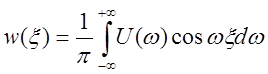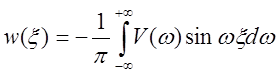Таким образом, физически возможная стационарная линейная система полностью определяется одной действительной (или одной мнимой) частью частотной характеристики.

Минимально-фазовые звенья и системы [1].

Если корни числителя и знаменателя передаточной функции лежат в левой полуплоскости, то такое звено называется минимально-фазовым. Для минимально-фазовых звеньев имеют место следующие соотношения (без доказательства):

, , .

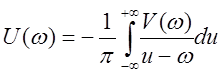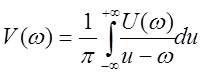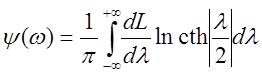Здесь , 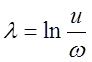. Таким образом, частотная передаточная функция минимально-фазового звена полностью определяется её вещественной  или мнимой частью , или модулем передаточной функции .

Логарифмические частотные характеристики.

          На практике обычно пользуются десятичными логарифмами и строят отдельно логарифмическую амплитудную частотную характеристику (ЛАХ) и логарифмическую фазовую частотную характеристику (ЛФХ).

Эта величина выражается в децибелах (дБ). Один Бел соответствует увеличению мощности в 10 раз. Так как  – отношение не мощностей, а напряжений (токов, перемещений и т.п.), то увеличение этого отношения в 10 раз будет соответствовать увеличению отношения мощностей в 100 раз, что соответствует двум Белам или 20 децибелам. Один децибел равен .