Диаграмма Вышнеградского [1, с.220].
Рассмотрим характеристическое уравнение третьего порядка:
![]() .
.
Нормированное уравнение:
![]() . Здесь
. Здесь ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Параметры А, В называются параметрами Вышнеградского.
Условия
устойчивости системы третьего порядка были сформулированы Вышнеградским в 1876
году (критерий Гурвица сформулирован в 1895). Эти условия имеют вид: ![]() ,
, ![]() ,
, ![]() .
.
Уравнение
границы колебательной устойчивости: ![]() – равнобокая гипербола.
Ниже изображена диаграмма Вышнеградского.
– равнобокая гипербола.
Ниже изображена диаграмма Вышнеградского.
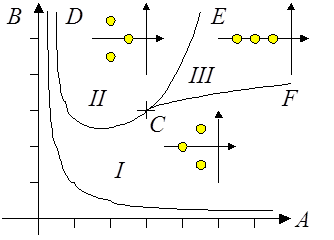
В точке С, где ![]() ,
, ![]() характеристическое
уравнение принимает вид
характеристическое
уравнение принимает вид ![]() .
.
В этой точке для исходного
уравнения ![]() .
.
Внутри области III дискриминант ![]() (область
трёх вещественных корней). В области I пара
комплексных корней лежит ближе к мнимой оси, чем вещественный корень, в области
II – наоборот. На границе между этими областями
все три корня лежат на одинаковом расстоянии от мнимой оси. Уравнение этой
границы можно найти, положив значения корней
(область
трёх вещественных корней). В области I пара
комплексных корней лежит ближе к мнимой оси, чем вещественный корень, в области
II – наоборот. На границе между этими областями
все три корня лежат на одинаковом расстоянии от мнимой оси. Уравнение этой
границы можно найти, положив значения корней ![]() ,
, ![]() :
:
![]()
![]() .
.
Приравнивание коэффициентов при одинаковых степенях даёт:
![]() ,
, ![]() ,
, ![]() .
.
Исключая ![]() и
и
![]() , имеем:
, имеем:
![]() ,
, ![]() .
.
Стабилизация радиального положения пучка в протонном синхротроне ТРАПП.
Уравнение движения пучка при наличии обратной связи:
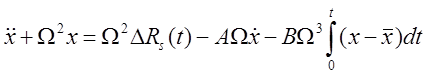
Динамика пучка самого по себе (объекта регулирования) описывается уравнением:
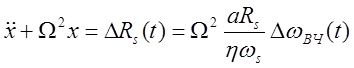 ,
, 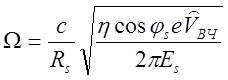 .
.
Здесь все возмущения (среднего магнитного поля, частоты и
амплитуды ускоряющего напряжения приведены к возмущению частоты, или – к
эквивалентному возмущению равновесного радиуса орбиты). Далее, для простоты, ![]() .
.
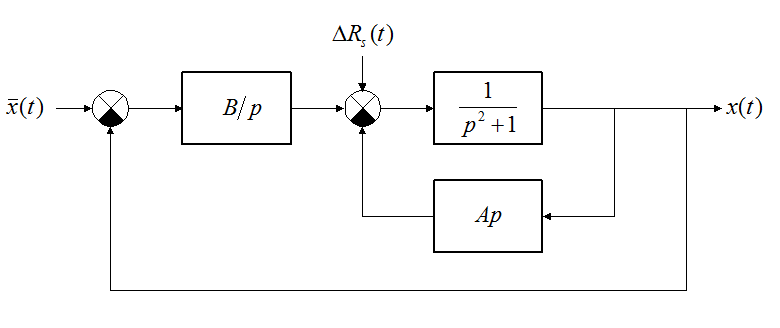
Петля по ![]() реализована
как петля обратной связи по отклонению фазы пучка от равновесной фазы.
Во-первых, это возможно в силу того обстоятельства, что
реализована
как петля обратной связи по отклонению фазы пучка от равновесной фазы.
Во-первых, это возможно в силу того обстоятельства, что ![]() ,
во-вторых, технически проще обеспечить широкую полосу пропускания этого тракта.
Коэффициент передачи разомкнутой системы:
,
во-вторых, технически проще обеспечить широкую полосу пропускания этого тракта.
Коэффициент передачи разомкнутой системы:
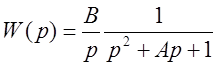 .
.
Характеристическое уравнение:
![]() .
.
Критерий Рауса-Гурвица даёт:
![]() ,
, ![]() ,
, ![]() .
.
На плоскости
параметров (![]() ,
,![]() ), в пределах области
устойчивости, корни характеристического уравнения имеют вид (
), в пределах области
устойчивости, корни характеристического уравнения имеют вид (![]() ,
, ![]() ):
):
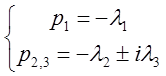 .
.
Структуру области
устойчивости удобно описывать параметрическими соотношениями, являющимися
результатом приравнивания коэффициентов уравнений ![]() :
:
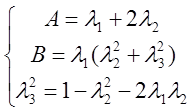 .
.
Ниже изображена структура области устойчивости.
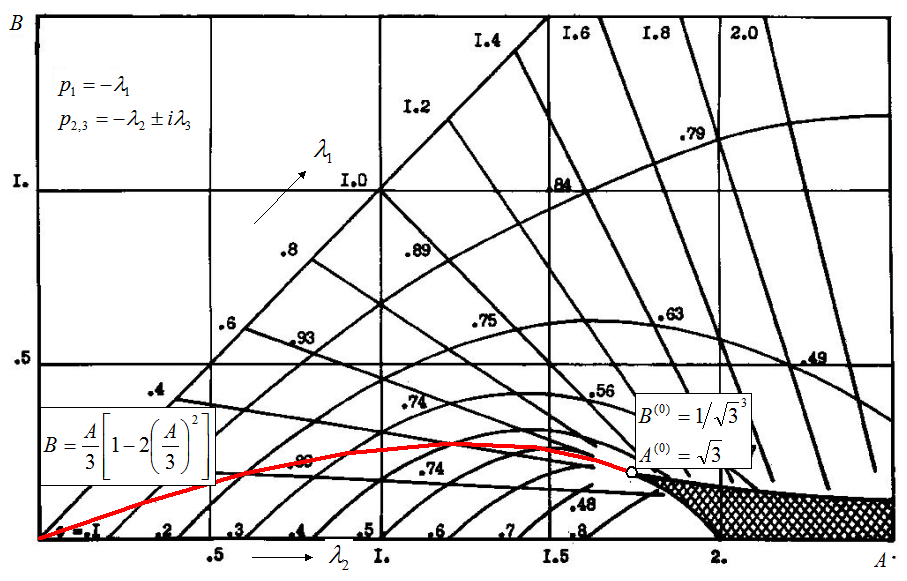
Если ![]() , то темпы ликвидации отклонения и
подавления колебаний равны, и можно говорить об общем темпе стабилизации
радиального положения пучка.
, то темпы ликвидации отклонения и
подавления колебаний равны, и можно говорить об общем темпе стабилизации
радиального положения пучка.
Равенство ![]() имеет место на следующей кривой:
имеет место на следующей кривой:
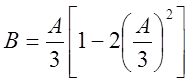 .
.
На этой кривой ![]() , т.е.
, т.е. ![]() ,
, ![]() и декремент
и декремент ![]() прямо
пропорциональны коэффициенту о.с. по фазе. Замечательным обстоятельством
является то, что по мере увеличения
прямо
пропорциональны коэффициенту о.с. по фазе. Замечательным обстоятельством
является то, что по мере увеличения ![]() ,
, ![]() вначале увеличивается, а затем должно
уменьшаться.
вначале увеличивается, а затем должно
уменьшаться.
В точке, где ![]() ,
, ![]() достигает
значения
достигает
значения ![]() . Соответствующий декремент
. Соответствующий декремент ![]() является в данном случае максимальным
декрементом. Т.е. не существует других корней характеристического уравнения,
чтобы абсолютные значения действительных частей всех из них были бы больше, чем
является в данном случае максимальным
декрементом. Т.е. не существует других корней характеристического уравнения,
чтобы абсолютные значения действительных частей всех из них были бы больше, чем
![]() .
.
Таким образом, максимальный темп стабилизации радиального положения пучка имеет место при следующих (оптимальных) значениях параметров петель о.с.:
![]() ,
, ![]() ,
,
когда все три корня характеристического уравнения одинаковы.
При ![]() и
и ![]() соответствующие
декременты имеют следующую величину:
соответствующие
декременты имеют следующую величину:
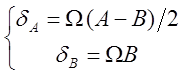 .
.
Таким образом, о.с.
по “радиальному положению”, как ей и положено, подавляет отклонение равновесного
радиуса, но при этом, в отсутствие о.с. по фазе (или, если угодно, по ![]() , что физически то же самое), раскачивает
синхротронные колебания.
, что физически то же самое), раскачивает
синхротронные колебания.
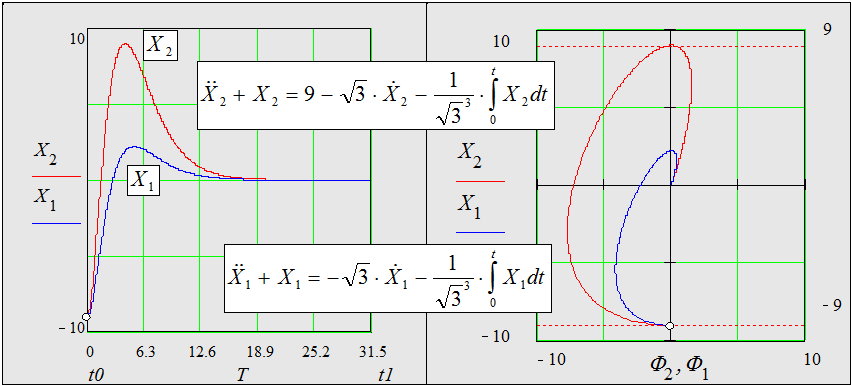
Ниже изображена
динамика системы при инжекции пучка с неравновесной энергией (![]() ), при равновесной (
), при равновесной (![]() )
и неравновесной (
)
и неравновесной (![]() ) частоте ускоряющего напряжения
(кривые
) частоте ускоряющего напряжения
(кривые ![]() и
и ![]() ,
соответственно). Видно, что система о.с. достаточно быстро стабилизирует
радиальное положение пучка, не позволяя ему покинуть пределы апертуры
,
соответственно). Видно, что система о.с. достаточно быстро стабилизирует
радиальное положение пучка, не позволяя ему покинуть пределы апертуры ![]() , при отклонениях энергии пучка и частоты
ускоряющего напряжения, соответствующих радиальному смещению пучка почти до
границ этой апертуры.
, при отклонениях энергии пучка и частоты
ускоряющего напряжения, соответствующих радиальному смещению пучка почти до
границ этой апертуры.
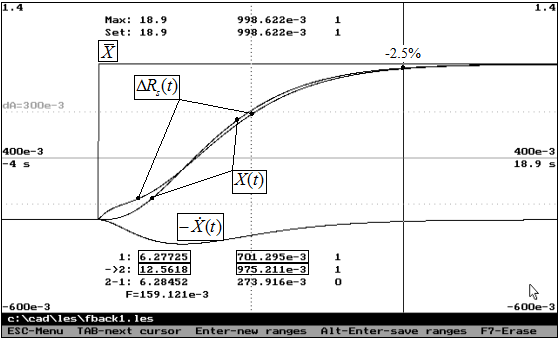
Ниже изображена реакция системы на ступенчатый сигнал управления радиальным положением пучка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.