Движение твердого тела с одной закрепленной точкой, страница 3

На основании (3.24.2) и (3.24.3) получим из уравнения (3.24.1) дифференциальное уравнение малых собственных колебаний системы с одной степенью свободы:

     (3.24.4).

Если разделить обе части уравнения (3.24.4) на а и обозначить положительную величину c/a=k², то получим уравнение колебаний в окончательной форме:

     (3.24.5).

Постоянная величина 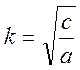 называется круговой (или циклической) частотой колебаний.

Дифференциальное уравнение (3.24.5) является однородным линейным уравнением второго порядка с постоянными коэффициентами. Его решение можно искать в виде q=e^lt. После подстановки в (3.24.5) получаем характеристическое уравнение

l²+k²=0.

Это квадратное уравнение имеет два чисто мнимых корня l_1,2=±ki. На основе теории дифференциальных уравнений решение уравнения (3.24.5) можно представить в виде:

q = C₁cos kt + C₂ sin kt                      (3.24.6)

и для обобщенной скорости

= -C₁ k sin kt + C₂ k cos kt             (3.24.7).

Произвольные постоянные С₁ и С₂ определяются из начальных условий  для обобщенной координаты и обобщенной скорости.

Используя начальные условия и выражения (3.24.6) и (3.24.7) получаем ;  подставляя это в (3.24.6) имеем

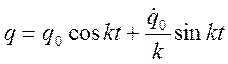                      (3.24.8)

Это одна из двух основных форм выражения собственных колебаний. Представим выражение для q в другой, так называемой амплитудной форме

q = A sin(kt+a).

Путем несложных вычислений можно получить, что 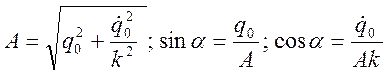. Величину А считают положительной и называют амплитудой колебаний, она определяет наибольшее отклонение обобщенной координаты от положения равновесия. Безразмерная постоянная a называется начальной фазой колебаний. Она является значением фазы колебаний (kt+a) при t=0 и может меняться в пределах от 0 до 2p.

Полученное нами решение представляет гармонические колебания системы с одной степенью свободы с периодом .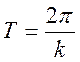

Добавим линейное сопротивление ( добавится к обобщенной силе) и опять же в предположении малости колебаний получим дифференциальное уравнение

         (3.24.9)

Приведем уравнение (3.24.9) к виду

       (3.24.10).

Постоянная k, как и раньше, является круговой частотой собственных колебаний системы без учета сопротивления, постоянная n=m/(2a) называется коэффициентом затухания.

Решение этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами опять же будем искать в виде q=e^lt.

Постоянная l определяется из характеристического уравнения l²+2nl+k²=0, которое получается после подстановки решения в дифференциальное уравнение.

Характеристическое уравнение имеет два корня:

l_1,2=               (3.24.11).

Могут представится три случая: 1) n < k – это случай малого сопротивления, 2) n>k – случай большого сопротивления и 3) n=k – случай критического сопротивления.

Если n<k, то величина под знаком квадратного корня в (11) отрицательна и обозначив через k₁²=можно получить решение уравнения (10) в виде

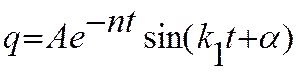          (3.24.12)

где постоянные A и a через начальные условия выразятся в следующей форме:

;

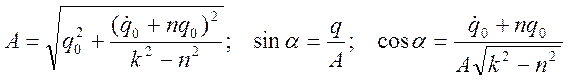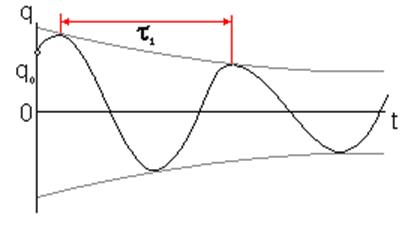Величина A положительна. Она не является амплитудой. Из графика видно, что величины наибольших последовательных наибольших отклонений q от положения равновесия уменьшаются с увеличением времени, стремясь к нулю при неограниченном возрастании времени. Имеем процесс, называемый затухающими колебаниями. Период затухающих колебаний

величина постоянная, не зависящая от начальных условий. Он больше периода собственных колебаний при отсутствии сопротивления .

            Если n>k (случай большого сопротивления) действительны и отрицательны, следовательно, общее решение дифференциального уравнения (3.24.10) имeет вид:

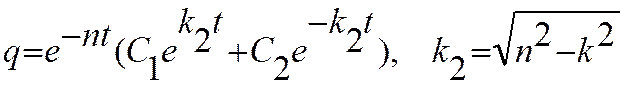    (3.24.13),

где С₁ и С₂ – произвольные постоянные, которые можно определить по начальным условиям.

Не выполняя вычислений, можно оценить поведение функции q(t), используя уравнение (3.24.13).

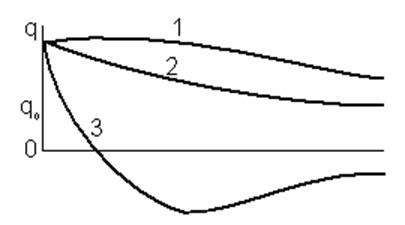
При  функция q(t) некоторое время возрастает до определенного максимума, а затем убывает, ассимптотически приближаясь к нулю [кривая 1]. При не очень больших по абсолютной величине отрицательных значениях может сразу начаться убывание q(t) [кривая 2]. При больших по модулю отрицательных значениях функция q(t), убывая, может достичь нулевого значения, соответствующего положению равновесия системы, стать отрицательной, ассимптотически приближаться к нулю [кривая 3]. Во всех этих случаях движение является затухающим, неколебательным, которое иногда называют также апериодическим.