Движение в центральном поле. Задача Кеплера, страница 2

При   радиус частицы не меняется, т.к. . Траектория, очевидно, представляет собой окружность. Поскольку частица движется по окружности, то центростремительная сила равна силе тяготения. Будем считать для простоты .  Тогда 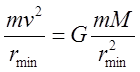. Помимо этого выполняется закон сохранения энергии: 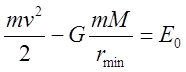. Сравнивая последние соотношения, убеждается, что 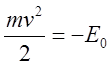, 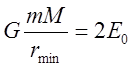. Другими словами на круговой траектории кинетическая энергия вдвое больше модуля потенциальной. 

Утверждается (без доказательства), что при  траектория представляет собой параболу. Нетрудно получить соотношения между «круговой: скоростью и

«параболической» на том же радиусе. Действительно: 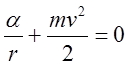,  отсюда параболическая скорость 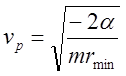. Учитывая, что круговая того – же радиуса: 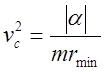получаем: .

Итак, зависимости от величины  имеются различные формы траекторий:

o   - эллиптическая траектория;

o   - параболическая траектория;

o   - гиперболическая;

o  - круговая, частный случай эллиптической траектории.

Определим параметры эллиптической траектории в зависимости от значений полной энергии - и момента импульса . Обе величины являются сохраняющимися, причем . Запишем уравнение сохранения энергии:

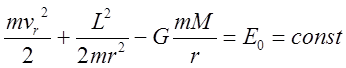.                        (9)

С учетом 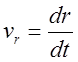и обращения  в точках P и A – см рис. n4.  (которые соответственно называются «перигелий», «апогелий». Пери - ближайшая к Солнцу точка траектории,  Апо – наиболее удаленная от Солнца точка) запишем уравнение (9) в безразмерном виде:

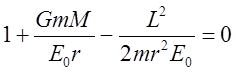.                   (10)

После обращения (10) в уравнение относительно :

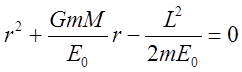                   (11)

Определим  решения (11) . Считаем, что начало координат помещено в массивном центре. Воспользовавшись свойством корней квадратного уравнения: 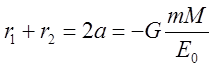, где  - длина большой полуоси эллипса. После введения 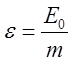- полной энергии на единицу массы частицы, получаем:

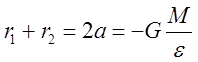.                         (12)

Обозначим - длина малой полуоси. Напомним, что . Легко показать согласно определению: . Последнее следует из перпендикулярности  и равенства в т. С. (см. рис. n5). Исходя из основного свойства эллипса – сумма расстояний от фокусов до любой точки равняется удвоенной большой полуоси запишем уравнение энергии в т. С:

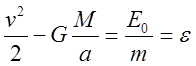. Подставляя (12) находим:

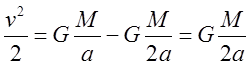, где - полная скорость в т. С, окончательно имеем: .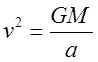

Покажем, что малая полуось зависит от момента импульса частицы и ее полной энергии. Учитывая 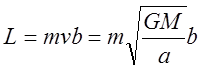 получаем: .

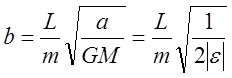Итак параметры эллиптической орбиты определяются значениями полной энергии частицы и момента импульса:

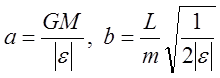                                  (13).

Сформулируем в заключении все три закона Кеплера.

1.  Все планеты движутся по эллипсам, в фокусе которого находится Солнце.

2.  Радиус вектор планеты за равные промежутки времени заметает равные площади. (постоянство секториальной скорости).

3.  Квадраты периодов обращения планет относятся как кубы больших полуосей.  .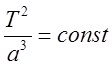

Получим последний закон Кеплера из ранее приведенных соотношений.  Напомним, что площадь эллипса суть . Учитывая постоянство секториальной скорости 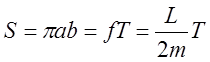. Подстановка значений  из (13) дает: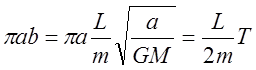. Отсюда после упрощений: 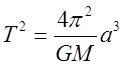, или окончательно:

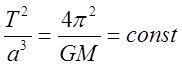                             (14)

        в (14) зависит только от параметров массивного центра (Солнца) и одинакова для всех планет.

Задача Резерфорда.

Проиллюстрируем одно из точных решений движения частицы в центральном поле в случае инфинитного движения. Решение этой задачи в свое время сыграло решающую роль в становлении планетарной модели атома – модели Резерфорда.

Рассмотрим движение легкой частицы, налетающей из бесконечности на массивный силовой центр. Будем называть прицельным параметром минимальное расстояние, на котором пролетела бы частица относительно массивного центра в отсутствие взаимодействия. (см. рис. n6.) Считаем, что частица и массивный центр взаимодействуют кулоновским образом, причем сила взаимодействия является отталкивающей. В реальном эксперименте наблюдалось рассеяние частиц на атомах золота.

Из геометрии следует: , или . Из уравнения сохранения энергии: 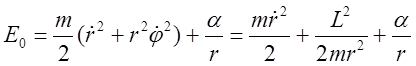 послое несложных алгебраических преобразований имеем: 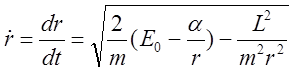. Разделяя переменные получаем:

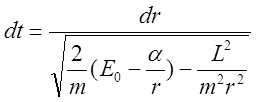. С учетом , или 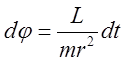 находим:

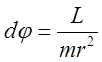
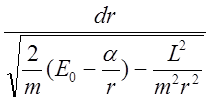                               (15)

Введем значения полной энергии и момента импульса частицы на бесконечности:

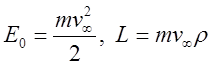. Подставляя сохраняющиеся величины  в (15) и интегрируя в пределах от минимального радиуса между частицей и силовым центром – () учитывая симметрию траектории находим :

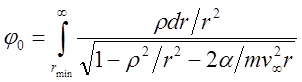.                                (16)

(16) есть табличный интеграл. После подстановок и упрощений находим:

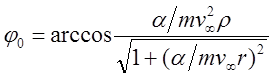
                                  (17)

Отсюда:

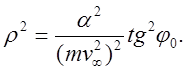  После подстановки 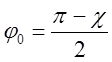формула преобразуется в:

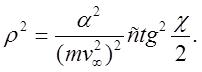                                     (18)

Полученное выражение называется формулой Резерфорда по имени нобелевского лауреата Э. Резерфорда. Чаще она приводится в равносильной форме:

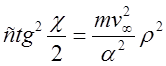.                                          (19)

Видно, что . При малых  угол отклонения стремится к .