Взаимодействие излучения с атомами и молекулами (Раздел 3 учебного пособия), страница 2

Таким образом, гамильтониан распадается на сумму независимых членов, каждый из которых содержит только . Каждый такой член соответствует бегущей волне с определенными  и поляризацией, причем имеет вид функции Гамильтона одномерного гармонического осциллятора. Поэтому о разложении (132) говорят, как о разложении поля на осцилляторы, рассматривая как оператор импульса 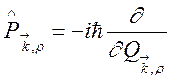, соответствующий нормальной координате . Поскольку гамильтониан (132) распадается на сумму независимых слагаемых, то энергия электромагнитного поля равна сумме энергий гармонических осцилляторов

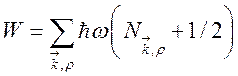,                               (133)

где  — целые числа, характеризующие число фотонов с заданными  и поляризацией в объеме .

С другой стороны, возвращаясь к выражению (127) для  и вновь используя (131), гамильтониан поля можно записать в виде

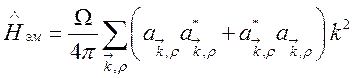.                        (134)

Волновая функция, описывающая состояние электромагнитного поля с  фотонами, должна иметь временную зависимость вида 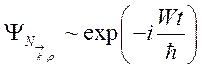, где энергия поля W (133) определяет зависимость волновой функции от числа фотонов .

Вычислим среднее значение энергии и приравняем его выражению (133) для W:

.

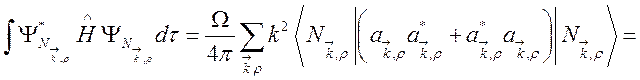
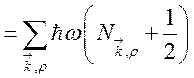Для матричного элемента находим:

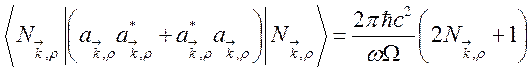.         (135)

Индексы  в операторах 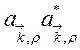и  мы в дальнейшем будем опускать и обозначать число фотонов .

Операторы  имеют смысл операторов рождения (излучения) и уничтожения (поглощения) фотонов. Как хорошо известно из теории гармонических осцилляторов [1, § 23], матричные элементы операторов 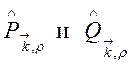, а следовательно  отличны от нуля только для переходов с изменением числа , то есть фактически при изменении числа фотонов на единицу. Действительно, вычислим матричный элемент

.

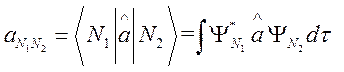Учитывая временную зависимость , получим

.

Видно, что для того, чтобы матричный элемент не зависел от времени в случае оператора  необходимо, чтобы конечное состояние поля содержало на один фотон данного сорта больше, чем начальное, а в случае оператора * необходимо выполнение обратного соотношения. То есть отличны от нуля матричные элементы вида  и .

Используя свойства матриц (см. [1], § 11), выражение (135), в котором присутствует матричный элемент произведения операторов, можно переписать в виде

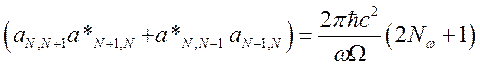.           (136)

Данное выражение устанавливает связь матричных элементов с разными N, причем, учитывая эрмитовость матриц, получим

.

Примем N = 0, что соответствует нормальному состоянию осциллятора. Соответственно,  нужно считать тождественно равным нулю. Последовательное применение уравнения (135) с =0,1,2... позволяет

найти

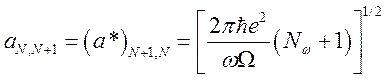.                  (137)

Вычислим вероятность  излучения фотона в единицу времени атомной системой с переходом ее из состояния j в состояние f [1,5]

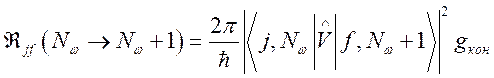,              (138)

где  оператор возмущения,  — число состояний, приходящихся на единичный интервал энергий в конечном состоянии. Выражение (137) получено с учетом выполнения закона сохранения энергии . Учитывая, что временная зависимость волновой функции фотонов в стационарном состоянии имеет вид: 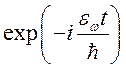, где  — полная энергия данного состояния с частотой w, равная , а оператор возмущения

                        ,

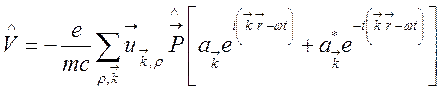где  — оператор импульса отдельного электрона, из (138) получим

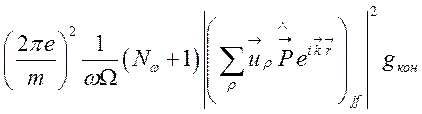.   (139)

Согласно (125) , что позволяет экспоненту  заменить единицей. Тогда, учитывая, что , имеем

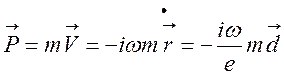,                                 (140)

где  — дипольный момент атома.

Из (139) с учетом (140) получим

.

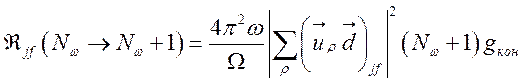Eсли конечным состоянием атомной системы является состояние дискретного спектра со статистическим весом , то [5]

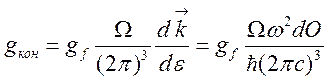,                           (141)

где dO — элемент телесного угла, характеризующий направление вектора . Усредняя по величине угла между векторами   и суммируя по двум поляризациям, для случая неполяризованного света получим окончательное выражение для вероятности излучения фотона

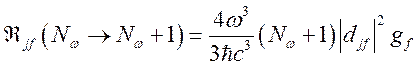.                    (142)

Подобным образом можно найти вероятность поглощения фотона

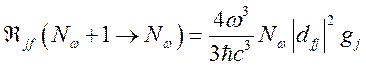.                        (143)

Очевидно, что при = 0 из (142) мы получаем вероятность спонтанного излучения атома.