The Harmonic Oscillator, страница 2

                    

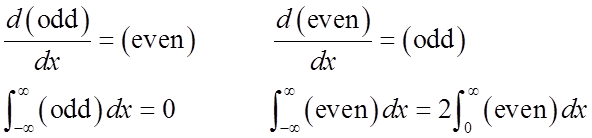
Just from symmetry:

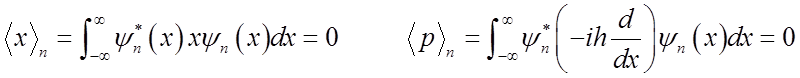
                                  odd                                                         odd

Average displacement & average momentum = 0

IR spectroscopy     Þ       H.O. selection rules

 

Intensity of vibrational absorption features          

 

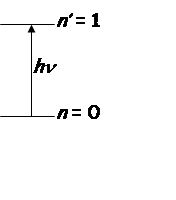Vibrational transition

Intensity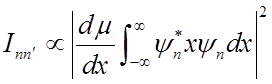    

1)       Dipole moment of molecule must change as molecule vibrates       Þ      

HCl can absorb IR radiation, but N₂, O₂, H₂ cannot.

2)       Only transitions with            allowed (selection rule).

                     (Prove for homework.)

QUANTUM MECHANICAL HARMONIC OSCILLATOR & TUNNELING       

E

Classical turning points

ET

Classical H.O.:        Total energy     

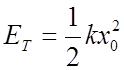
oscillates between K and U.

Maximum displacement x₀ occurs when

-x0

x0

x

all the energy is potential.

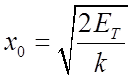  is the “classical turning point”

The classical oscillator with energy E_T can never exceed this displacement, since if it did it would have more potential energy than the total energy.

QM H.O.

 

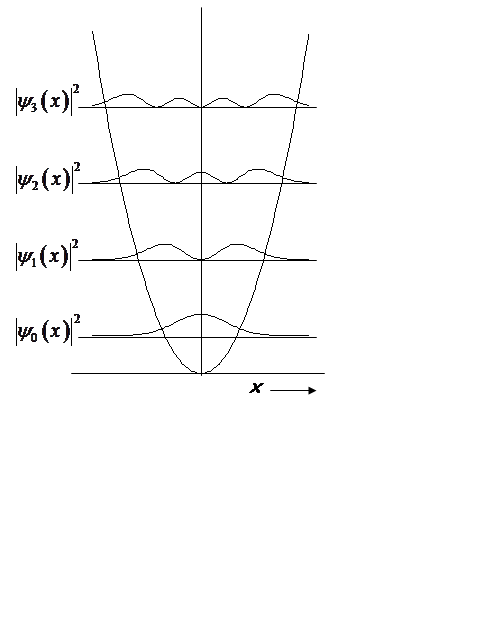
At high n, probability density begins to look classical, peaking at turning points.

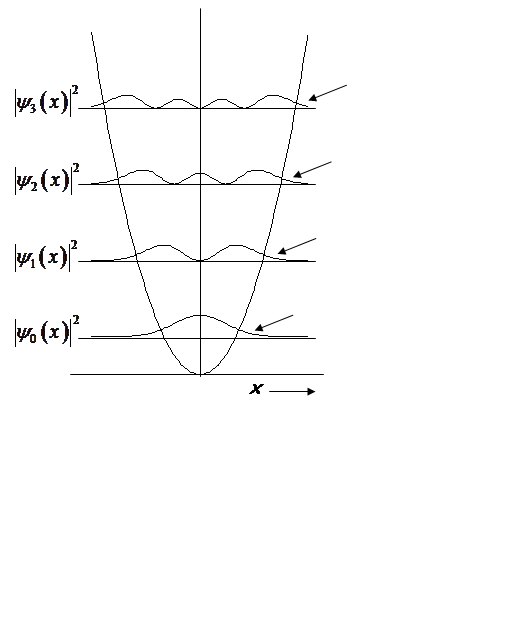
Non-zero probability at x > x₀!

Prob. of (x > x₀, x < -x₀):

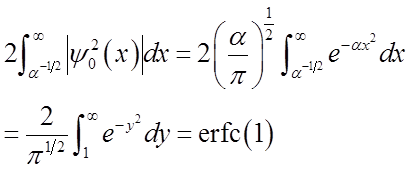“Complementary error function”

tabulated or calculated numerically

Prob. of (x > x₀, x < -x₀) = erfc(1) = 0.16

Significant probability!

The oscillator is “tunneling” into the classically forbidden region. This is a purely QM phenomenon!

Tunneling is a general feature of QM systems, especially those with very low mass like e- and H.

 

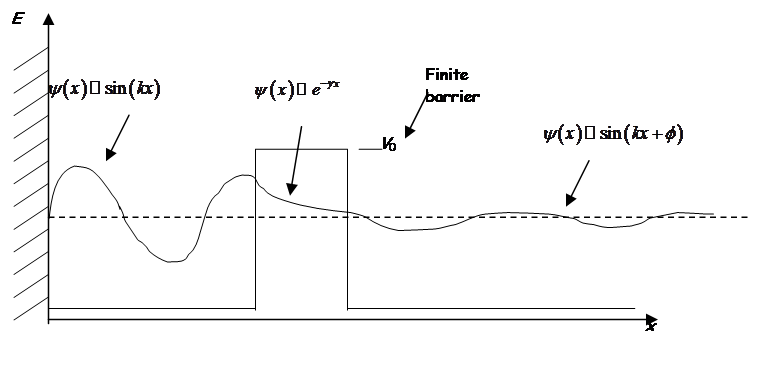
Even though the energy is less than the barrier height, the wavefunction is nonzero within the barrier! So a particle on the left may escape or “tunnel” into the right hand side.

Inside barrier: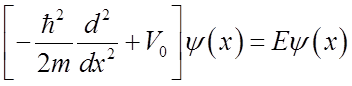      

                     or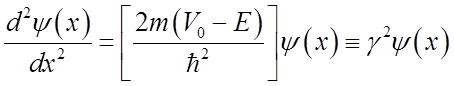      

Solutions are of the form          

Note            

If barrier is not too much higher then the energy and if the mass is light, then tunneling is significant.

Important for protons (e.g. H-bond fluctuations, tautomerization)

Important for electrons (e.g. scanning tunneling microscopy)

Nonstationary states of the QM H.O.

System may be in a state other than an eigenstate, e.g.

      with     (normalization),  e.g.         

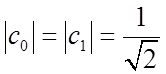
Full time-dependent eigenstates can be written as

      

where

System is then time-dependent:

          What is probability density?

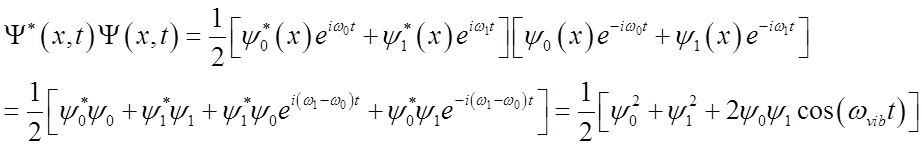
Probability density oscillates at the vibrational frequency!

 

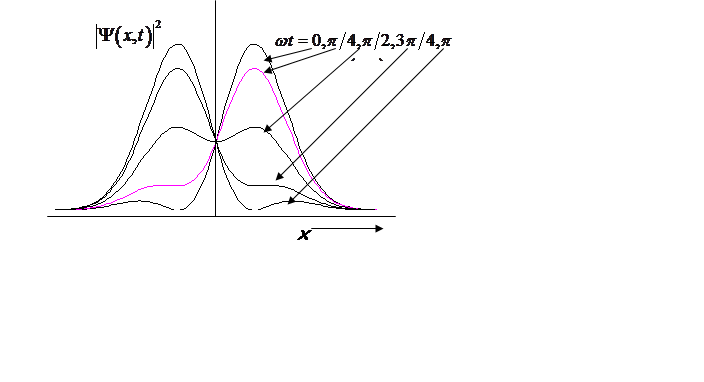What happens to the expectation value <x>?

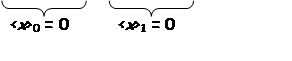
<x>(t) oscillates at the vibrational frequency, like the classical H.O.!

Vibrational amplitude is  

\  

Relations among Hermite polynomials

Recall H.O. wavefunctions

 

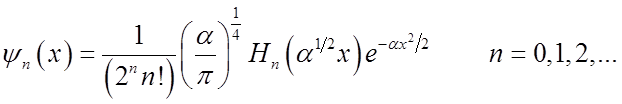
                     Normalization                   Gaussian

Hermite polynomial

Generating formula for all the H_n:

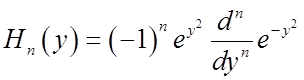
A useful derivative formula is:

Another useful relation among the H_n’s is the recursion formula:

Substituting    above gives

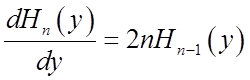
Use these relations to solve for momentum <p>(t)

<p>0 = 0

<p>1 = 0

\ 

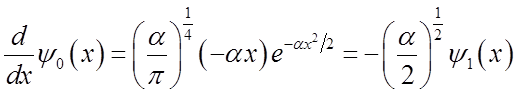
To solve integral 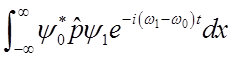  use relations among H_n’s

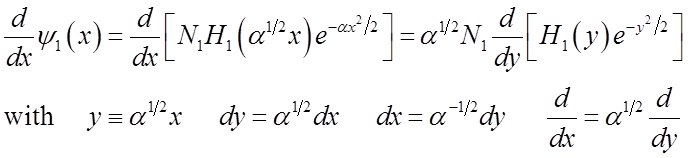
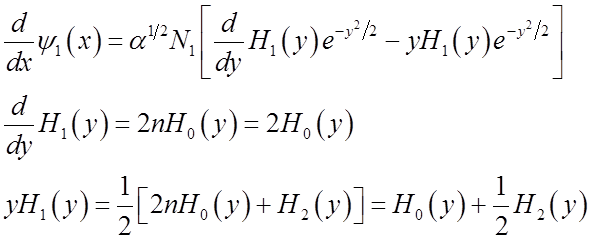
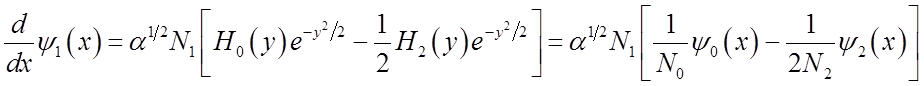
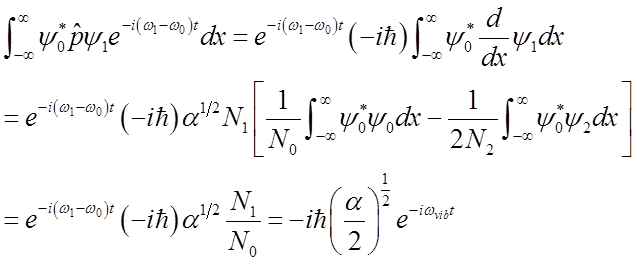
Finally

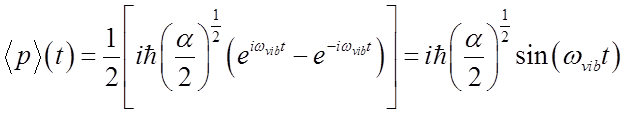
Average momentum also oscillates at the vibrational frequency.