Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 6

6) .

После преобразования получим:

.             (2.4)

Вынесем общий множитель :

.     (2.5) 

Для физически реализуемых устойчивых цепей частотный коэффициент передачи и операторный коэффициент передачи связаны.

Заменим, оператор  на  в выражении и получим:

.  (2.6)

Преобразуем:

.(2.7)

Воспользуемся формулами Эйлера:

   ;

С учетом этих формул получим:

,                                        (2.8) 

,                             (2.9) 

                   .                                   (2.10)

Подставим формулы (2.8) – (2.10) в выражение для спектральной плотности входного сигнала:

.         (2.11)

Вынесем общий множитель:                  

.            .(2.12)

Произведем ряд тригонометрических преобразований. Воспользуемся формулой суммы синусов и формулой двойного угла

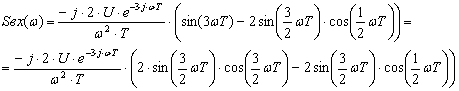(2.13)        

и вынесем  за скобку:

.                  (2.14)        

Преобразуем выражение в скобках, воспользовавшись формулой разности косинусов:

.                  (2.15)        

После всех преобразований получили выражение для спектральной плотности:

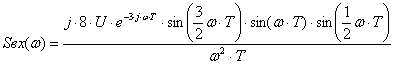.              (2.16)        

2.2 Амплитудный и фазовый спектры входного сигнала

Модуль  - есть амплитудный спектр входного сигнала:

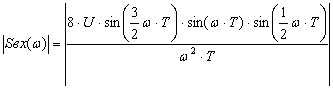.                 (2.17)

График амплитудного спектра приведён на рисунке 2.1

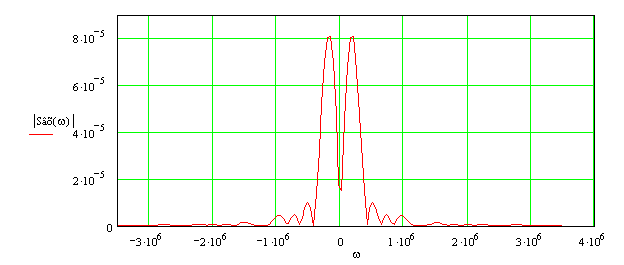
Рис. 2.1 - Амплитудный спектр входного сигнала.

Фазовый спектр это аргумент от спектральной плотности :

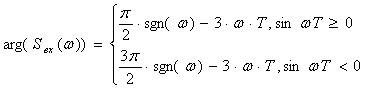(2.18)

График фазового спектра приведён на рисунке 2.2

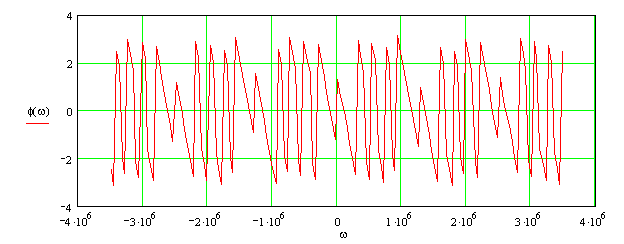
Рис. 2.2 - Фазовый спектр входного сигнала.

2.3 Определение ширины спектра входного сигнала

Ширина спектра определится из графика (Рисунок (2.3)). Проводится уровень 0,1 от максимального значения и определяется последнее пересечение графика с этим уровнем. Считая, что ширина спектра равна целому числу полуволн, находим :

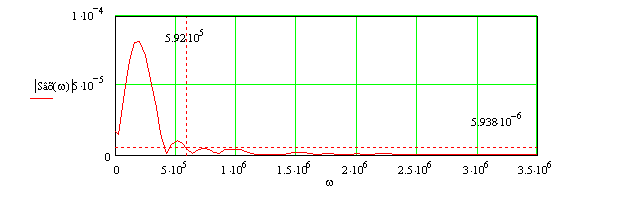
Рисунок 2.3 – Определение ширины спектра входного сигнала