Определение тепловых свойств твердых тел методом регулярного режима: Методические указания к лабораторной работе

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ И НАУКЕ

Филиал государственного образовательного учреждения

высшего профессионального образования

«Московский энергетический институт

(технический университет)»

в г. Волжском

Кафедра «Промышленная теплоэнергетика»

С.Б. Шевцова

ОПРЕДЕЛЕНИЕ ТЕПЛОВЫХ СВОЙСТВ ТВЕРДЫХ ТЕЛ МЕТОДОМ РЕГУЛЯРНОГО РЕЖИМА

Методические указания к лабораторной работе

ВОЛЖСКИЙ 2008

УДК 536.2

ББК 31.31

Рецензент:

Староверов В.В. – канд. техн. наук, доцент кафедры ПТЭ

ГОУ ВПО «МЭИ (ТУ)» в г. Волжском

Определение тепловых свойств твердых тел методом регулярного режима: Методические указания к лабораторной работе /Сост. Шевцова С. Б. – Волжский: Филиал ГОУ ВПО «МЭИ (ТУ)» в г. Волжском, 2008. -    с.

Предлагаемые методические указания позволяют закрепить теоретические знания в области нестационарной теплопроводности, ознакомиться с методикой экспериментального определения коэффициента температуропроводности материала методом регулярного режима.

Методические указания к лабораторной работе иллюстрированы графиками и рисунками, изложены в доступной форме со ссылками на литературные источники. Являются хорошей учебной базой для представления данного раздела программного курса студентам всех технических специальностей очной и очно – заочной (вечерней) форм обучения теплоэнергетического факультета.

Печатаются по решению Учебно-методического совета филиала ГОУ ВПО «МЭИ (ТУ)» в г. Волжском.

УДК 536.2

ББК 31.31

                                                               Шевцова С. Б., 2008

Филиал ГОУ ВПО «МЭИ (ТУ)»

                                                              в г. Волжском, 2008

1. ЦЕЛЬ РАБОТЫ

Изучение теории нестационарной теплопроводности отдельных стадий этого процесса, закономерностей температурного поля, признаков регулярной стадии; ознакомление с экспериментами.

2. СОДЕРЖАНИЕ РАБОТЫ

Определение теплопроводности и температуропроводности теплоизоляционного материала при невысоких температурах.

3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

В общем случае поле температур охлаждаемого или нагреваемого тела определяются начальным тепловым состоянием тела, его физическими свойствами, геометрической формой и размерами, а также условиями теплообмена с окружающей средой, то есть описывается уравнением теплопроводности (уравнением Фурье - Кирхгофа), [1, с.360]:

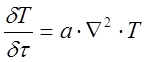,                                             (3.1)

где   – температура тела как функция координат и времени (t);

а– коэффициент температуропроводности.

Поле температур определяется начальным тепловым состоянием тела – начальными условиями.

                                            (3.2)

условиями теплообмена с окружающей средой (граничными условиями)

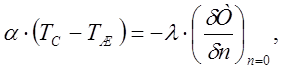                                       (3.3)

где – коэффициент теплоотдачи от поверхности тела к окружающей среде;

          – температура поверхности тела;

          – температура окружающей среды (жидкости);

          – коэффициент теплопроводности тела;

n– нормаль к поверхности тела.

Решение уравнения (3.1) для случая  представляется в виде ряда:

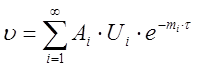,                                         (3.4)

где  – избыточная температура тела по отношению к жидкости;

– постоянные, определяемые формой тела и начальными условиями;

 – функции координат, характеризующие пространственное распределение температуры и содержащие в качестве параметров физические постоянные;

 – постоянные, представляющие ряд положительных возрастающих чисел, зависящих от геометрии тела, его физических свойств, условий теплообмена тела с окружающей средой и не зависящих от начального распределения температур, координат и времени.

С увеличением  ряд (3.4) быстро сходится и по истечении некоторого времени ,определяемого значением критерия Фурье 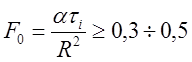  ( – характерный размер образца) упорядоченный режим нагревания (охлаждения) образца, при котором поле температур перестает зависеть от начального распределения температуры в теле. В этом случае можно ограничиться первым членом ряда и считать:

,                                               (3.5)

где m – темп нагревания (охлаждения) образца.

Из (3.5) следует, что:

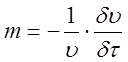.                                                     (3.6)

Таким образом, темп нагревания (охлаждения) характеризует  относительную скорость изменения избыточной температуры в любой точке тела в единицу времени. Независимость координат этой точки от времени называется регулярным режимом.

Для регулярного режима из уравнения (3.5) легко получить:

­­,                                             (3.7)

где  ­­– постоянная.

Зависимость логарифма избыточной температуры от времени прогрева для любой (произвольной) точки в теле представлена на рисунке 3.1.

График

 

Рис. 3.1

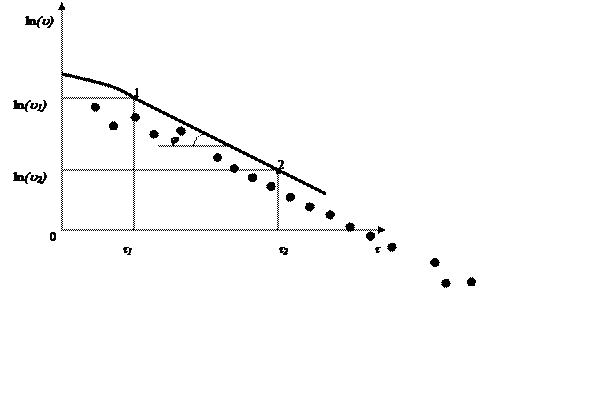(1 – 2) – линейный участок, соответствующий регулярному режиму.

Для 0 <t <t₁ имеем переходный режим. Распределение температур в теле определяется начальными условиями и описывается рядом (3.4).