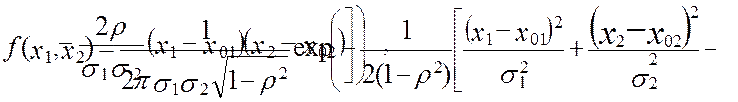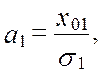
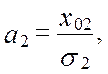
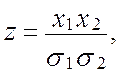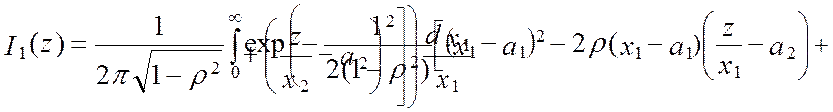Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 6

где x₀₁, x₀₂ – математические ожидания, s₁, s₂ - дисперсии случайных величин x₁, x₂, r - корреляционный момент случайных величин x₁, x_2.

              Выражение плотности вероятности произведения z=x₁x₂ двух коррелированных  нормальных случайных величин получится, если произвести замену переменных:

Интеграл I₂(z) , вычисляется   в пределах (-¥, 0). Очевидно, что плотность вероятности произведения не всегда соответствует нормальному распределению. Дифференцируемая функция в достаточно узких пределах изменения аргументов может быть приближенно заменена линейной. При этом ошибка, возникающая при линеаризации, тем меньше, чем уже границы изменения аргументов и чем ближе функция к линейной. Ошибка линеаризации, безусловно, влияет на точность конечной математической модели, однако ее величина может быть оценена и отнесена к методической погрешности при использовании модели. Итак, линеаризации подвергается функция N переменных: Y(Y₁,Y₂,...,Y_N)=Y₁Y₂...Y_N, где Y₁, Y₂, ...,Y_N – случайные величины, представляющие собой текущие значения случайных функций Y₁(t), Y₂(t), ..., Y_N(t) в некоторый произвольный момент времени. Допуская, что сигналы Y_i(t) являются стационарными эргодическими случайными процессами произведём линеаризация функции Y(Y₁,Y₂,...,Y_N) путем разложения в ряд Тейлора в окрестности точки     М(М₁,М₂,...,М_N), где М₁, М₂, ..., М_N  - математические ожидания случайных величин Y₁, Y₂, ...,Y_N, с сохранением в разложении лишь членов первого порядка: Y(Y₁, Y₂, ...,Y_N)»Y(M₁, M₂, ...,M_N)+ 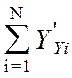(M₁, M₂, ...,M_N)(Y_i-M_i), где  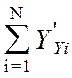(M₁, M₂, ...,M_N ) -значение первой частной производной функции Y(Y₁, Y₂, ...,Y_N) по переменной Y_i  в точке М. Или:

Y(Y₁, Y₂, ...,Y_N) » M₁ M₂ ...M_N+M₂M₃...M_N (Y₁-M₁)+M₁M₃...M_N (Y₂-M₂) + ...

                        + M₁M₂...M_N-1 (Y_N-M_N)=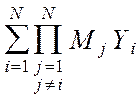- (N-1)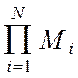.      (2.34)

Выражение (2.34) представляет собой линеаризованную в окрестности рабочей точки М уравнения измерения критерия управления Y(Y₁, Y₂, ...,Y_N) и именно это выражение (2.34) мы будем использовать в дальнейшем для анализа метрологических характеристик робастных систем и их информационно-измерительных подсистем.

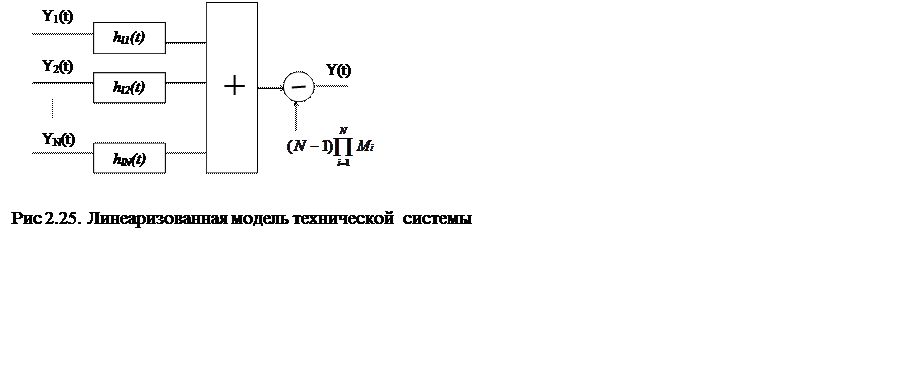
        Таким образом, нелинейное взаимодействие измерительной информации  в робастных системах заменено на аддитивное. Обобщенная структура линеаризованной информационно-измерительной системы, при этом, будет выглядеть так, как это представлено на рисунке 2.25 [24]. Из схемы видно, что замена нелинейного взаимодействия измерительных каналов в рамках информационно-измерительной системы на аддитивное, сопровождается появлением в структуре каждого канала дополнительного динамического  звена, характеризующегося весовой функцией h_li(t).

 

Весовая функция дополнительного линейного динамического звена позволяет выразить реакцию этого объекта Y(t) на некоторое входное воздействие X(t) как [20]: 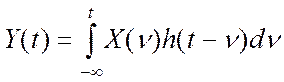.  Откуда следует, что весовая функция h_li(t) дополнительно появляющегося звена определяется следующим образом:  h_li(t)=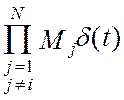, где d (t)=  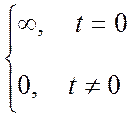- функция Дирака [20].  Введя обозначение    A_i=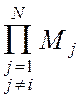,        можно весовую функцию дополнительно появляющегося звена записать как : h_li(t)=A_id(t).

        Необходимо отметить, также, появление в линеаризованной системе (см. рис.2.25) сигнала 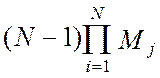, который аддитивно наложен на выходной сигнал технической системы системы.  Его отсутствие приводит к тому, что реакция линеаризованной системы, на некоторое совокупное входное воздействие Y₁(t), Y₂(t), ..., Y_N(t) будет отличаться по математическому ожиданию от реакции исходной измерительной системы на такое же воздействие, то есть  на величину этого сигнала.

              Эффективность рассматриваемого метода линеаризации может вызывать сомнения в связи с тем, что диапазон изменения случайных аргументов не настолько мал, чтобы в его пределах функция могла быть с достаточной точностью линеаризована. Однако, оценку погрешности, вносимой операцией линеаризации, можно осуществить, сохранив в разложении функции не только линейные члены, но и некоторые члены более высокого порядка. Погрешность линеаризации в таком случае будет выражаться как разность характеристик случайной функции, полученных при ее разложении в ряд Тейлора с несколькими членами и разложении в ряд Тейлора только с линейными членами. Тогда разложение функции Y =f ( Y₁, Y₂, …, Y_N )  в ряд Тейлора, в окрестности точки М (М₁, М₂ ,..., М_N), при сохранениии в разложении членов не выше второго порядка, имеем приближенно: