Нехай F – многозначне відображення,
F: Х×У→ Х×У, що визначається співвідношенням
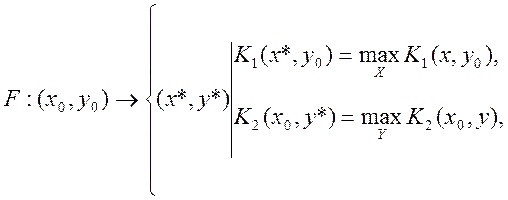
тобто образ відображення F складається з пар найкращих відповідей гравців на стратегії y0 та x0 відповідно
Функції К1 та К2 як математичні сподівання виграшів в ситуації (х,у) білінійні по х і у, а отже, образ F(x0,y0) ситуації (х0,у0) при відображенні F представляє собою випуклу компактну множину в Х×У. Більше того, якщо послідовність пар {(xn0, yn0)}, (xn0, yn0) ÎX×Y та {(x∕n, y∕n)}, (x∕n, y∕n) ÎF(xn0, yn0) мають граничні точки, тобто
![]()
то в силу білінійності функцій К1 і К2 і компактності множин Х та У маємо, що (x∕, y∕) ÎF(x0, y0). Тоді за теоремою Какутані існує ситуація (х*,у*) Х×У, для якої (х*,у*)ÎF(х*,у*), тобто
К1(х*,у*)≥К1(х,у*), К2(х*,у*)≥К2(х*,у) , "хÎХ, "уÎУ. Доведено.
Множина Парето.
Розглянемо множину точок Ω на площині (U,V). Точки цієї множини розподіляються на внутрішні ( такі точки які належать, разом з точками будь якої малої округи) та граничні точки ( в будь якій околиці яких є і внутрішні точки і точки , що не належать Ω). Точки множини Ω розіб’ємо на 3 класи (див. рис.3.5) :
1. До першого класу відносяться точки, які можна зрушити з місця так, щоб збільшити при цьому обидві її координати і при цьому точка залишиться в множині Ω (до цього класу відносяться всі внутрішні точки і частина граничних);
2. Другий клас утворюють точки, зміщенням яких по множині Ω можна збільшити тільки одну з координат при зберіганні значення другої (вертикальний відрізок АВ та горизонтальний відрізок PQ на границі множини ).
3. В третій клас потрапляють такі точки ( точки дуги BQ границі області), зміщення яких по множині Ω не в змозі збільшити жодної координати точки.
|
|
Рисунок 3.5. Множина точок області Ω.
Множину точок третього класу називають множиною Парето даної множини Ω.
……………………………………………..…….?
3.5 Резюме
þ@Як бачимо, і для рівноваги Неша, і для оптимуму Парето, можуть бути ситуації дещо «парадоксального» характеру!
Більш того: «найгіршим» є те, що таких рішень одна й та ж сама гра може нам запропонувати декілька! Так яку ж стратегію нам вибрати? Яку рекомендацію надати? Який прогноз зробити у цьому випадку?
þ@Підсумки розділу зручно представити рисунком, на якому співставленні різні концепції рішення ігор двох осіб з довільною сумою виграшів (некооперативні ігри). На рис. 3.5 подаються множини рішень різних концепцій. Якщо одна з множин є включенням іншої, то вона «більш точна» за нею, тобто, якщо перша концепція визначає деяку ситуації гри в якості рішення, то це означає, що друга концепція визначить цю ситуацію, як одне із рішень гри.
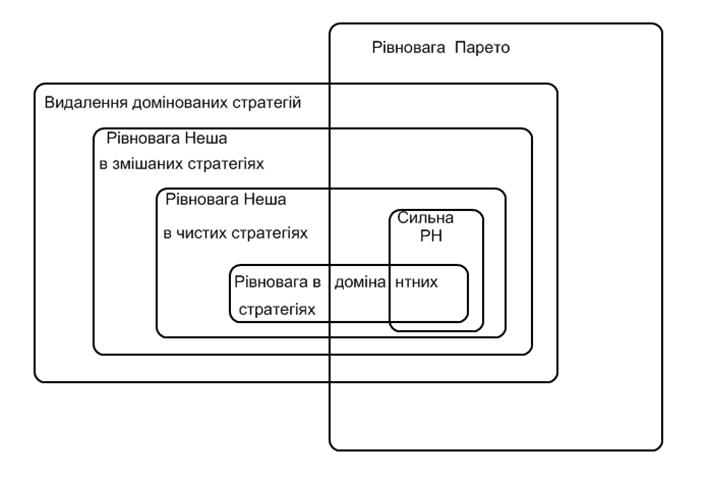
Рисунок Порівняння концепцій рішення некооперативних ігор.
 3.6 Завдання до розділу „Біматричні ігри”
3.6 Завдання до розділу „Біматричні ігри”
 Визначити оптимальні стратегії та виграші гравців в неантагоністичній
грі та здійснити порівняльний аналіз методів розв’язку . Виконати роботу за
методами:
Визначити оптимальні стратегії та виграші гравців в неантагоністичній
грі та здійснити порівняльний аналіз методів розв’язку . Виконати роботу за
методами:
§ Метод математичного аналізу.
§ Метод фіктивного розігрування.
§ Метод Монте-Карло.
§ Метод направленого перебору.
§ Метод Лемке- Хаусона.
Варіанти завдань матриці гри.
№1 №2
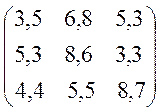
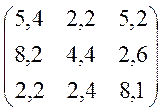
№3 №4
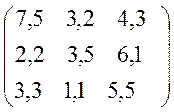
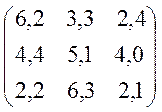
№5 №6
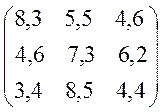
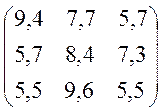
№7 №8
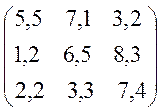
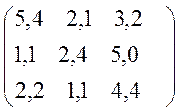
№9 №10
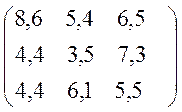
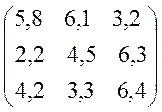
№11 №12
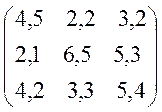
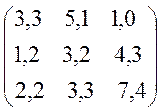
№13 №14
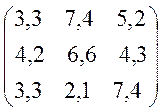
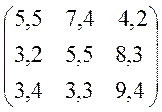
№15 №16
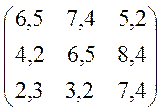
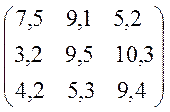
№17 №18
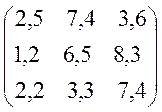
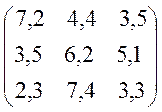
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.