Ігри двох осіб з довільною сумою, страница 8

Ця множина є фундаментальним симплексом (відрізком) в просторі. R². Вона представлена на рисунку 3.2. Кожній змішаної стратегії другого гравця поставимо у відповідність вибрані чисті стратегії другого і першого гравців. Тут вибрані чисті стратегії першого гравця відзначені відповідно 1,2,3,  а у другого гравця стратегії відзначені, як 4,5.  Кожній змішаної стратегії другого гравця відповідають, по-перше, чисті стратегії другого гравця, що в цій змішаної стратегії використовуються з ймовірністю 0, по-друге, чисті стратегії першого гравця, що є найкращими відповідями на цю дію другого. Так як біматрична гра невиродженою, то кожній змішаній стратегії другого гравця в підсумку буде відповідати не більше, ніж дві чисті стратегії (першого і другого гравців). Для знаходження найкращих чистих відповідей першого гравця розглянемо його варіанти вибору в залежності від змішаної стратегії другого гравця

.

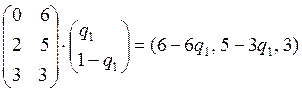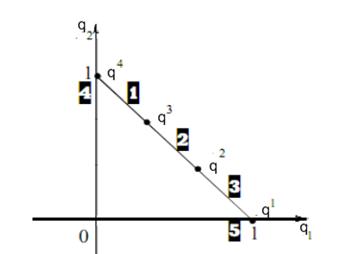
Рисунок 3.2. Вибір змішаних стратегій у біматричній грі з позицій гравця В.

 Перший гравець вибирає свою чисту стратегію, щоб отримати найбільший виграш. Цей виграш визначається функціями

f₁(q₁) = 6-6q₁,f₂(q₁) = 5-3q₁,f₃(q₁) = 3.

З рис. 3.3 видно, що для q₁Î[0,1/3] буде виконуватись f₁(q₁)  ≥ f₂(q₁) і f₁(q₁)  ≥ f₃(q₁). У цьому випадку перший гравець вибирає свою першу стратегію 1.

Для q₁Î[1/3, 2/3] маємо  f₂(q₁)  ≥ f₁(q₁) і f₂(q₁)  ≥ f₃(q₁). Перший гравець обирає свою чисту стратегію 2. І, нарешті, для  q₁Î[2/3,1] вибирається стратегія 3.

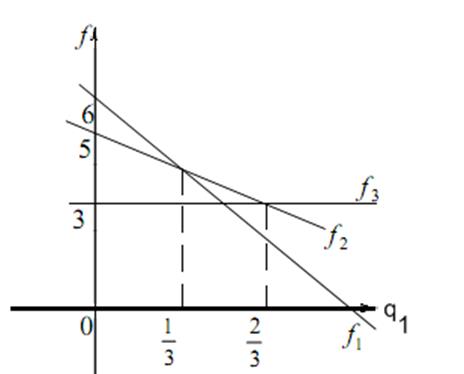
Рисунок 3.3. Відповідність між стратегіями другого і першого гравця

Виділимо ті стратегії другого гравця, яким відповідає дві чисті стратегії. З рис. 3.2 випливає, що це будуть

q¹ = (1, 0) → (3,,5);

q² = (2/3, 1/3) → (2 , 3);

q³ = (1/3, 2/3) → (1,2);

q⁴ = (0, 1) → (1,4);

Розглянемо ситуацію, складені з виділених стратегій першого і другого гравців. Кожній з них буде відповідати набір чистих стратегій, як об'єднання відповідних чистих стратегій гравців для цієї ситуації. Тоді ситуація буде рівновагою по Нешу (РН) тоді і тільки тоді, коли їй буде відповідати повний набір всіх чистих стратегій у грі. Дійсно, в цьому випадку кожна чиста стратегія або не використовується в рівновазі, або є найкращою відповіддю на вибір іншого гравця. Така ситуація і є рівноважною. У даній грі виділено п'ять стратегій першого гравця та чотири стратегії у другого. Тоді розглядається 20 ситуацій. Три з них підходять під умову РН. Дійсно,

(p^*, q^*) = (p⁵, q¹) = ((0, 0, 1), (1, 0))→((1,2, 4));(3,,5));

(p^*, q^*) = (p⁴, q²) = ((0, 1/3, 2/3), (2/3, 1/3))→(( 1,4,5)); (2 , 3));

(p^*, q^*) = (p², q³) = ((2/3, 1/3, 0), (1/3, 2/3))→(( 3, ,4, 5) ; (1,2)).

Обчислимо виграші гравців в рівноважних ситуаціях

F^*(p^*, q^*) = F^*(p⁵, q¹) = (υ_A, υ_B) = (p^*TAq^*, p^*TBq^*) = (3, 4);

F^*(p^*, q^*) = F^*(p⁴, q²) = (υ_A, υ_B) = (p^*TAq^*, p^*TBq^*) = (3, 8/3);

F^*(p^*, q^*) = F^*(p², q³) = (υ_A, υ_B) = (p^*TAq^*, p^*TBq^*) = (4, 2/3);

Таким чином, в розглянутому прикладі є три рівноваги по Нешу.

@……………………...............................................  Математичний відступ.

Доведення теореми 3.1.

Проблема існування РН пов’язана з аналізом найкращих відповідей     Best_i (s_-i) ={s^*_i ÎS_i | K_i(s^*_i,s_-i) ≥ K_i(s_i,s_-i), "s_iÎS_i}

гравця і на профіль стратегій s_-i  всіх інших учасників.

          Складемо профіль найкращих відповідей всіх гравців

Best (s)={ Best_i (s_-i),iÎN }. Очевидно, що s^* є РН тоді і тільки тоді, коли s^*Î Best (s^*). Таким чином, існування РН зв’язано з існуванням нерухомих точок відображення Best (s).

Розглянемо відображення F: SÞS, яке кожну точку sÎS (ситуацію гри) переводить в множину Best (s). Це відображення являє собою неперервне відображення опуклого компакту в себе. Якщо воно буде замкненим ( або полунеперервним зверху), то за теоремою Какутані, в нього існує нерухома точка s^* Î F, яка зрозуміло й буде РН.

          Покажемо це для біматричної гри.

Множини змішаних стратегій Х та У гравців являють собою опуклі многогранники ( симплекси), тому множина ситуацій Х×У –компактна опукла множина.