Ігри двох осіб з довільною сумою, страница 7

          Тим не менше, при всіх привабливих рисах сильного РН, його використання обмежено тим, що навіть у змішаних стратегіях воно існує не у всіх іграх.

3.3 Алгоритм Лемке-Хаусона

У більш загальному випадку біматрічной гри ситуація рівноваги по Нешу обчислюється з використанням різних лінійних методів, що мають своєю основою завдання лінійного програмування. Історично, одна з перших підходів розроблений на початку 60-х років. Це відомий алгоритм Лемке - Хаусона знаходження рішення в біматрічной грі. У ситуації рівноваги гри двох осіб мішана стратегія одного гравця урівноважує виграш другого гравця при використанні їм чистих стратегій.

Нехай матриці А, В мають розміри m × n. Будемо розглядати невироджену біматричну гру. Біматрічная гра  називається невиродженою, якщо для кожної вихідної стратегії першого (другого) гравця число чистих стратегій, що є найкращим відповіддю другого (першого) гравця, не перевершує числа стратегій з спектру вихідної стратегії, першого (другого) гравця.

Розглянемо застосування алгоритму Лемке - Хаусона для знаходження рівноваг в не виродженій біматричній грі на прикладі.

Приклад 3.2. Вирішити біматричну гру, задану матрицями виграшу гравців А та В, використовуючи алгоритм Лемке – Хаусона

.

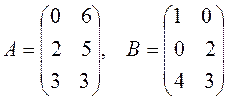У даній біматричній грі у гравців немає домінуючих стратегій. Але в грі маємо РН в чистих стратегіях - РН(p*, q*) = ((0, 0, 1), (1, 0)) ∈ X×Y;  f(p*, q*) = (3, 4).

Знайдемо рішення в змішаних стратегіях.. Проведемо міркування з боку першого гравця. Множину його змішаних стратегій позначимо

S_A={(p₁,p₂,1-p₁-p₂) | p₁,p₂Î[0,1], p₁+p₂≤1}

Ця множина є фундаментальним симплекс в просторі. R³. Вона представлена на рисунку 3.1. Кожній змішаної стратегії першого гравця поставимо у відповідність вибрані чисті стратегії першого і другого гравців. Чисті стратегії першого гравця будемо відзначати 1, 2, 3, а чисті стратегії другого гравця відзначимо 4,5. Кожній змішаної стратегії першого гравця поставимо у відповідність, по-перше, чисті стратегії першого гравця, що в цій змішаної стратегії використовуються з ймовірністю 0, по-друге, чисті стратегії другого гравця, що є найкращими відповідями на цю дію першого. Так як біматрична гра невироджена, то кожній змішаній стратегії першого гравця в підсумку буде відповідати не більше, ніж три чисті стратегії (першого і другого гравців). Для знаходження найкращих чистих відповідей другого гравця розглянемо його варіанти вибору в залежності від змішаної стратегії першого

 

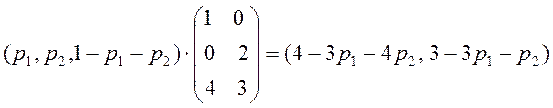
Визначимо ті стратегії першого гравця, на які другий гравець відповідає першій чистої стратегією. У цьому випадку, 4-3p₁-4p₂≥3-3p₁-p₂, і, отже,. p₂ ≤ 1/3. Для змішаних стратегій з такою умовою обираємо першу чисту стратегію другого гравця. Для інших стратегій першого гравця (тобто стратегій з умовою  p₂≥ 1/3) вибираємо друге чистий стратегію другого гравця. Результати виборів зображені на рис. 3.1.

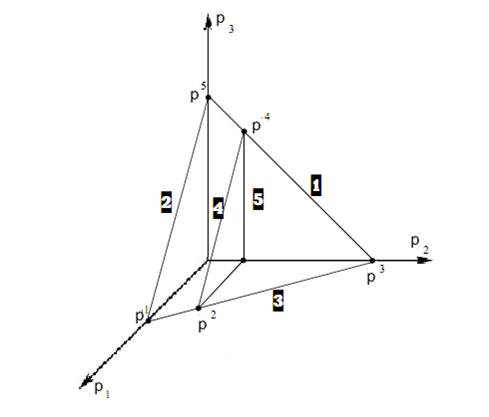
Рисунок 3.1. Вибір змішаних стратегій з позицій гравця А.

Вибрані чисті стратегії першого гравця відзначені відповідно 1,2,3, а у другого гравця стратегії відзначені, як 4,5. Виділимо ті стратегії першого гравця, яким відповідає три чисті стратегії. З рис. 3.1 слідує, що це будуть

P¹ = (1,0,0) → (2 , 3, ,4));

P² = (2/3,1/3,0) → ( 3, ,4, 5));

P³ = (0,1,0) → (1, 3,,5)

P⁴ = (0,1/3,2/3) → ( 1,4,5));

P⁵ = (0,0,1) → (1,2, 4));

Проведемо аналогічні міркування з боку другого гравця. Множину його змішаних стратегій позначимо

S_B={(q₁, 1-q₁) | q₁Î[0,1]}.