Числове розв’язання нелінійних рівнянь. Відображення множин. Теореми про стискаючі відображення, страница 7

  Нехай  – корінь, що підлягає визначенню. Будемо вважати, що вхідними даними для задачі обчислення кореня є значення функції . Оскільки  обчислюється наближено, то позначимо функцію, отриману в дійсності через . Припустимо, що в малому околі кореня виконується нерівність: . Для близьких до  значень х справедлива рівність , отже, 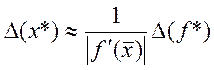. Це означає, що число обумовленості задачі знаходження кореня дорівнює 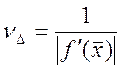. З останньої формули можна зробити висновок, що чим менше значення похідної функції в точці кореня, тим задача гірше обумовлена. Зокрема, задача знаходження кратного кореня має число обумовленості – нескінченність.

  Інтервал невизначеності кореня. Якщо функція  неперервна, то знайдеться такий малий окіл  кореня , що має радіус ε, у якому виконується нерівність . Це означає, що для  знак обчисленого значення  взагалі не зобов’язаний збігатися зі знаком , і, отже, стає неможливим визначити, яке саме значення х з інтервалу  обертає функцію f в нуль. Цей інтервал називається інтервалом невизначеності кореня. Очевидно, що радіус інтервалу невизначеності для простого кореня дорівнює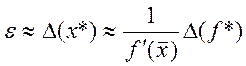. Аналогічно можна показати, що для кратного кореня 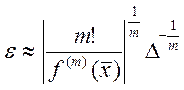. Це означає, що для простого кореня радіус інтервалу невизначеності прямо пропорційний похибці обчислення функції , а для кратного кореня .

  Приклад. Теоретична оцінка радіуса інтервалу невизначеності кореня.

  Нехай . Корінь рівняння простий і дорівнює . Тоді  і . Якщо , то . Це означає , що знайти корінь із точністю меншою, ніж радіус інтервалу невизначеності, не вдасться.

2.9  Метод Ньютона для знаходження кратного кореня

  Метод Ньютона на випадок кратного кореня має лише лінійну швидкість збіжності. Щоб зберегти квадратичну збіжність, його модифікують у такий спосіб:

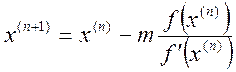, де m – кратність кореня. Як правило, значення m невідоме. Використовуючи метод Ньютона, можна знайти кратність кореня. Для цього будемо задавати значення m = 1,2,3 і обчислювати значення кореня із заданою точністю, одночасно підраховуючи кількість ітерацій для кожного значення m. При деякому значенні m число ітерацій буде мінімальним. Це значення m і є кратністю кореня.

Питання та завдання до розділу 2

1     Постановка задачі розв’язання нелінійних рівнянь. Основні етапи розв’язання задачі.

2     Ітераційне уточнення кореня: порядок збіжності методу, апріорні й апостеріорні оцінки похибки.

3     Метод бісекції: опис методу, швидкість збіжності, критерій закінчення.

4     Метод простої ітерації розв’язку нелінійного рівняння: опис методу, умова й швидкість збіжності, критерій закінчення, геометрична ілюстрація, приведення до вигляду, зручного для ітерацій.

5     Метод Ньютона розв’язку нелінійного рівняння: опис методу, теорема про збіжність, критерій закінчення, геометрична ілюстрація.

6     Недоліки методу Ньютона. Модифікації методу Ньютона. Модифікація методу Ньютона для пошуку кратних коренів.

7     Інтервал невизначеності кореня.

8     Визначити кількість коренів рівняння й для кожного кореня знайти відрізки локалізації:
 a) , b) .

9     Знайти дійсний корінь рівняння    методом бісекції з точністю .

10  Визначити порядок  p і знаменник q  швидкості збіжності методу бісекції.

11  Виписати ітераційну формулу і вказати початкове наближення для розв’язку рівняння

.

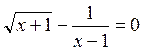12  Рівняння    має 2 корені: ,   . Для уточнення кореня застосовується метод простої ітерації 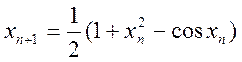. До якого кореня зійдеться процес? Запропонувати ітераційний процес для уточнення другого кореня.

13  Розв’язується рівняння  . Визначити, який з ітераційних процесів збігається до кореня:                 ,
                                         ,
                                         .

14  Нехай рівняння  f(x)=0   має на відрізку  [a,b]  єдиний корінь x і для його обчислення використається метод  простої ітерації  . Показати, що якщо   - неперервна функція на [a,b] і  на ньому, то для будь-якого початкового наближення з відрізка локалізації  ітераційна послідовність збігається до кореня.