Числове розв’язання нелінійних рівнянь. Відображення множин. Теореми про стискаючі відображення, страница 3

Уже на прикладі алгебраїчного многочлена відомо, що нулі f(х) можуть бути як дійсними, так і комплексними. Тому більш точною є постановка задачі у визначенні коренів рівняння (2.7), розміщених у заданій області комплексної площини. Можна розглядати задачу визначення дійсних коренів, розміщених на заданому відрізку. Іноді, нехтуючи точністю формулювань, будемо говорити, що потрібно розв’язати рівняння (2.7).

У загальному випадку задача визначення коренів рівняння (2.7), як правило, розв’язується в два етапи. На першому етапі вивчається розміщення корені і проводиться їх відділення, тобто виділяються області в комплексній площині, що містять тільки один корінь. Крім того, вивчається питання про кратність коренів.  Знаходяться деякі початкові наближення для коренів рівняння (2.7). На другому етапі, використовуючи задане початкове наближення, будується ітераційний процес, що дозволяє уточнити значення невідомого кореня.

Не існує якихось загальних регулярних прийомів розв’язання задачі про розміщення коренів довільної функції f(х). Найбільш повно вивчене питання про розміщення коренів алгебраїчних многочленів

              f(x)=a₀+a₁x+a₂x²+…+a_mx^m.                   (2.8)

Наприклад відомо, що якщо для многочлена (2.8) з дійсними коефіцієнтами виконані нерівності f(c)>0,f’(c)>0,…,f^(m)(c)>0, то додатні корені f(х) не перевершують числа с. Дійсно, з формули Тейлора

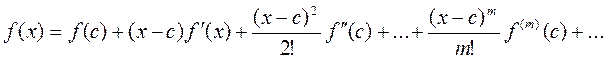
одержуємо, що f(x)>0 при x>c.

Чисельні методи розв’язання нелінійних рівнянь є, як правило, ітераційними методами, що припускають завдання досить близьких до шуканого розв’язку початкових даних. Перш ніж переходити до викладу конкретних ітераційних методів, відзначимо два прості прийоми відділення дійсних коренів рівняння (2.7). Припустимо, що f(х) визначена і неперервна на [а,b].

Перший прийом полягає в тому, що обчислюється таблиця значень функції f(х) у заданих точках х_kÎ[а, b], k=0, 1,..., п. Якщо виявиться, що при якомусь к числа f(х_k), f(x_k+1) мають різні знаки, то це буде означати, що на інтервалі (х_k,x_k+1) рівняння (2.7) має принаймні один дійсний корінь (точніше, має непарне число коренів на (х_k, x_k+1)). Потім можна розбити інтервал (x_k,x_k+1) на більш дрібні інтервали і за допомогою аналогічної процедури уточнити розміщення кореня.

Більш регулярним способом відділення дійсних коренів є метод бісекції (розподілу навпіл). Припустимо, що на (а, b) роміщений лише один корінь х рівняння (2.7). Тоді f(а) і f(b) мають різні знаки. Нехай для визначеності f(а)>0, f(b)<0. Покладемо x₀=0,5×(a+b) і обчислимо f(x₀). Якщо f(x₀)<0, то шуканий корінь знаходиться на інтервалі (a,x₀), якщо ж f(х₀)>0, то  на (х₀, b). Далі, із двох інтервалів (a,x₀) і (х₀,b) вибираємо той, на кінцях якого функція f(х) має різні знаки, знаходимо точку х₁-середину обраного інтервалу, обчислюємо f(х₁) і повторюємо зазначений процес. У результаті одержуємо послідовність інтервалів, що містять шуканий корінь х_1, причому довжина кожного наступного інтервалу вдвічі менша за попередній. Процес закінчується, коли довжина знову отриманого інтервалу стане менше заданого числа e>0, і за корінь х приблизно береться середина цього інтервалу.

Помітимо, що якщо на (а, b) міститься кілька коренів, то зазначений процес зійдеться до одного з коренів, але заздалегідь невідомо, до якого саме. Можна використовувати прийом виділення коренів: якщо корінь х=х^* кратності m знайдений, то розглядається функція g(х)=f(х)/(x-x^*)^т і для неї повторюється процес визначення кореня.

                          y

                   

                          O        ax^*b                            x

                     

Рис. - 2.1

Обмеження кореня функції, якщо вона визначення на необмеженому інтервалі здійснюється так.

1 Для початкового наближення x₀, знайти f₀=f(x₀), задати інтервал пошуку D і його інкремент d>1.

2 Обчислити a=x₀-D, b=x₀+D; f_a = f(a), f_b = f(b).

3 Збільшити інтервал пошуку: D=Dd.