З цією метою вводять поняття класу-сусіда, або ж класу, реалізації котрого є найближчими до поточного класу. Фізично це є клас з найменшою міжцентровою відстанню до поточного класу.
Таким чином, для розрахунку оптимального радіусу необхідно для кожного класу знайти його сусіда, і безпосередньо переходити до оптимізації радіусу. Пари класів сусідів логічно описати у вигляді масиву
Para[i]=k, де k-номер класа- сусіда i-того класу розпізнавання.
Алгоритм розрахунку масиву PARA наступний.
1. Обрати номер класу i.
2. знайти міжцентрові відстані від еталонного вектора і-того класу до решти класів.
3. Обрати з пункту 2 мінімальну міжцентрову відстань, що відповідає класу к.
4. Занести число к в і-ту позицію масиву PARA.
Після того, як ми визначили клас-сусід для кожного з класів, переходимо до розрахунку оптимальних радіусів.
Беремо якийсь з класів.
Обираємо певне значення радіусу j, наприклад рівним числу 5, та визначаємо точні сні характеристики.
От наприклад нам треба розрахувати к1.тобто кількість реалізацій, що потрапляють в контейнер.
Що означає «реалізація потрапляє в контейнер»? Це означає, що кодова відстань від неї до еталонного менша або дорівнює поточному радіусу.
Тобто ми порівнюємо відстані до реалізацій з поточним радіусом та дивимося, скільки з них менша або рівна поточному значенню радіуса j.
І навпаки, к2- це кількість реалізацій нашого класу, що не потрапила в контейнер. Тобто загальна кількість реалізацій нашого класу мінус к1.
Що ми можемо спостерегти?
При порівнянні незмінними є відстані від реалізацій поточного класу до еталонного вектору поточного класу(та відстані від реалізацій чужого класу до еталонного вектору поточного класу при розрахункові к3 та к4). Змінюються лише точні сні характеристики в залежності від значення радіусу контейнера, що покроково перебирається.
Отже, ми можемо один раз розрахувати кодові відстані до реалізацій, та на кожному кроці розрахунку точнісних характеристик порівнювати готові відстані з поточним значенням радіусу.
В цьому і є необхідність створення масиву кодових відстаней.
Масив кодових відстаней має таку структуру
SK[1..m][1..2][1...n1]
Фактично це m двовимірних масивів ,в котрих містяться відстані до своїх та до чужих реалізацій.
Розрахунок масиву пара наступний.
1. обрати клас, для котрого буде розраховуватися кодові відстані(до своїх та до чужих)
2.знайти відстані між еталонним вектором поточного класу та всіма реалізаціями поточного класу. Записати їх в масив.
3. знайти відстані між еталонним вектором поточного класу та всіма реалізаціями класа-сусіда . Записати їх в масив.
Оскільки кожна з точнісних характеристик може змінюватися
від 0(коли жодна з реалізацій не потрапила в контейнер) до ![]() (коли всі реалізації одного класу
потрапили контейнер даного класу), то поділивши цю величину на
(коли всі реалізації одного класу
потрапили контейнер даного класу), то поділивши цю величину на ![]() , отримаємо величину, що по аналогії з
імовірністю, може змінюватися від 0 до 1.
, отримаємо величину, що по аналогії з
імовірністю, може змінюватися від 0 до 1.
Такі характеристики мають наступні пояснення:
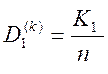 - перша достовірність, або
імовірність того, що свої реалізації будуть розпізнані як свої.
- перша достовірність, або
імовірність того, що свої реалізації будуть розпізнані як свої.
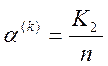 - помилка першого роду, або
імовірність того, що свої реалізації не будуть розпізнані як свої.
- помилка першого роду, або
імовірність того, що свої реалізації не будуть розпізнані як свої.
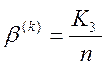 - помилка другого роду, або
імовірність того, що чужі реалізації будуть розпізнані як свої.
- помилка другого роду, або
імовірність того, що чужі реалізації будуть розпізнані як свої.
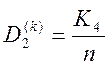 - друга достовірність, або імовірність
того, що чужі реалізації будуть розпізнані як чужі.
- друга достовірність, або імовірність
того, що чужі реалізації будуть розпізнані як чужі.
Функції інформаційних критеріїв оптимізації за Шенноном та за Кульбаком мають такий вигляд:
Ентропійна міра Шеннона:
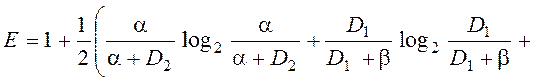
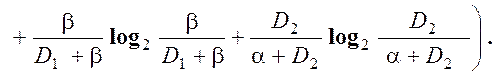
Інформаційна міра Кульбака:
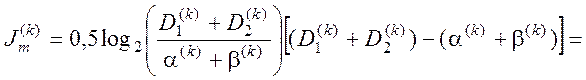
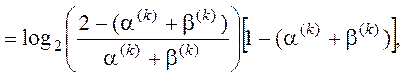
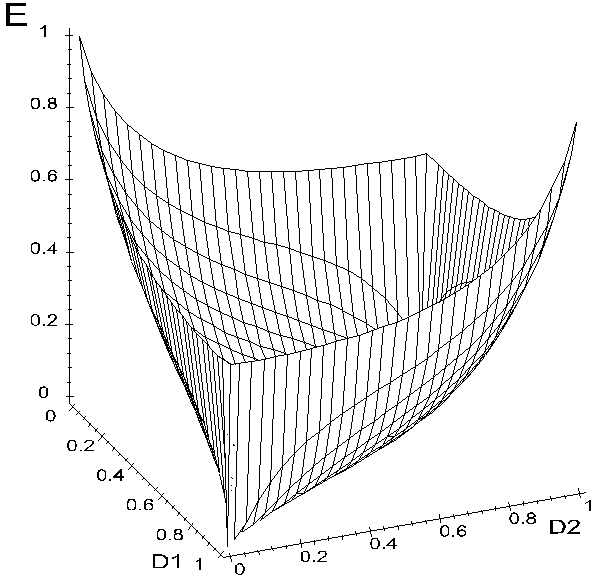
Задача розрахунку оптимального радіусу контейнеру означає вибір такого радіусу, при котрому функція КФЕ приймає максимальне значення . Але дані функції мають одну важливу особливість. Розглянемо для прикладу тривимірне представлення функції КФЕ за Шенноном, від таких параметрів як перша та друга достовірність.
У загальному випадку побудований
графік функції ![]() є поверхнею у тривимірному просторі (рис.5).
є поверхнею у тривимірному просторі (рис.5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.