Розв’язування систем лінійних алгебраїчних рівнянь (Лабораторна робота № 1)

Міністерство освіти і науки України

Сумський державний університет

Кафедра інформатики

Лабораторна робота №1

з дисципліни

«Чисельні методи»

на тему:

«Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР)»

Варіант 10

Підготувала

студент ІН-91

Татарченко А. С.

Перевірила

Назаренко Л.Д.

Суми 2011

1. Постановка задачі

Методом  Зейделя  розв’язати систему лінійних  алгебраїчних рівнянь  вигляду АХ=В із точністю до 0,0001.Визначити міру обумовленості системи та вплив похибки вхідних даних на результат.

	-1,00	0,22	-0,11	0,34	-2,7
10	0,38	-1,00	-0,12	0,22	1,5
	0,11	0,23	-1,00	0,51	-1,2
	0,17	-0,21	0,31	-1,00	0,17

2. Математичне обґрунтування та вибір алгоритму розв’язку

Для того, щоб система була сумісною, необхідно і достатньо, щоб ранг матриці системи співпадав із рангом розширеної матриці. (теорема Кронекера-Капеллі).

          Система має один розв’язок, коли дорівнює кількості невідомих. ;

          Якщо  менше кількості невідомих – система має безліч розв’язків.

За допомогою пакету Maple знаходимо, що

> det(A);

> A:= matrix(4, 4, [-1.00, 0.22, -0.11, 0.34, 0.38, -1.00, -0.12, 0.22, 0.11, 0.23, -1.00, 0.51, 0.17, -0.21, 0.31, -1.00]);

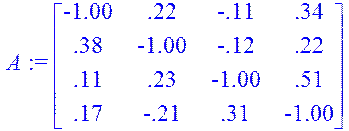
вхідна матриця

> rank(A);

ранг матриці А

> > B:= matrix(4, 5, [-1.00, 0.22, -0.11, 0.34,-2.7, 0.38, -1.00, -0.12, 0.22, 1.5, 0.11, 0.23, -1.00, 0.51,-1.2, 0.17, -0.21, 0.31, -1.00, 0.17]);

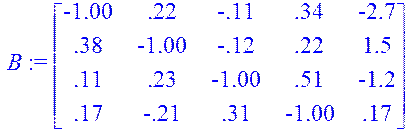
вхідна розширена матриця

> rank(B);

ранг матриці В

> coldim(A);

кількість змінних у СЛАР

Оскільки ранг матриці дорівнює рангу розширеної матриці і кількості невідомих у системі (кількість стовпців матриці визначає кількість невідомих), то ми можемо зробити висновок, що система є сумісною і має один розв’язок.

Для того, щоб ми могли використати метод Зейделя, для знаходження наближеного розв’язку системи, ми повинні перевірити достатню умову збіжності ітераційного процесу:

1.

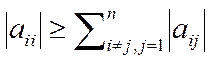
Легко переконатися, що

|-1.00|>|0.22|+|-0.11|+|0.34|

|-1.00|>|0.38|+|-0.12|+|0.22|

|-1.00|>|0.11|+|0.23|+|0.51|

|-1.00|>|0.17|+|-0.21|+|0.31|

Діагональна перевага елементів вихідної матриці СЛАР гарантує збіжність методу Зейделя.

2.  Визначимо міру обумовленості матриці А за формулою:

condA = ||A^-1||*||A||.

Якщо міра обумовленості матриці набагато більша за одиницю, то матриця є погано обумовленою, якщо ж міра обумовленості наближається до одиниці, то матриця добре обумовлена.

> cond(A);

condA=4. Оскільки condA>1, то дана матриця є погано обумовленою.

Похибка:

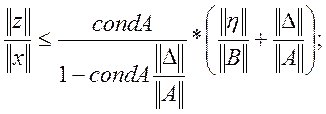
> cond(A);

> eta:= matrix(4, 1, [0.01, 0.01, 0.01, 0.01]);

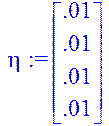
> delta:= matrix(4, 4, [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01,

> 0.01, 0.01, 0.01, 0.01]);

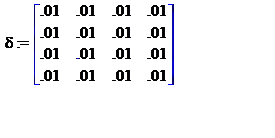
> norm(delta);

>  norm(B);

> norm(A);

> norm(eta);

 > (4.508114552/(1-4.508114552*0.04/1.85))*(0.01/4.37+0.04/1.85);

Відносна похибка впливу вхідних данних на результат складає 12%, що є не надто великою похибкою.

За допомогою пакету Maple, знайдемо власні чисела та перевіримо систему на стійкість. 

> eigenvectors(A);

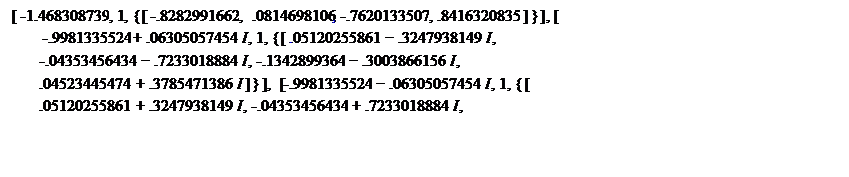
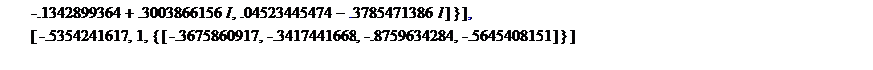
Так як модулы деяких власних чисел виходять за відрізок [-1;1], то система не є стійкою.

3.  Програмна реалізація

 #include<stdio.h>

#include<conio.h>

#include<stdlib.h>

#include<math.h>

void main()

{

 float A[4][4]={-1.00, 0.22, -0.11, 0.34, 0.38, -1.00, -0.12, 0.22, 0.11, 0.23, -1.00, 0.51, 0.17, -0.21, 0.31, -1.00 },

B[4]={-2.7, 1.5, -1.2, 0.17},C[4][4],D[4],X0[4],X1[4],max,eps=0.0001;

 int i,j;

 clrscr();

 puts("Matrica A:");

 for(i=0;i<4;i++)

  {for(j=0;j<4;j++)

   printf("%2.2f ",A[i][j]);

   printf("\n");}

 puts("Matrica B:");

 for(i=0;i<4;i++)

  printf("%2.2f ",B[i]);

 printf("\n");

 for(i=0;i<4;i++)

  for(j=0;j<4;j++)

   if (i==j) C[i][j]=0; else C[i][j]=-A[i][j]/A[i][i];

 puts("Matrica C:");

 for(i=0;i<4;i++)

  {for(j=0;j<4;j++)

   printf("%f ",C[i][j]);

   printf("\n");}

 puts("");

 for(i=0;i<4;i++)

  D[i]=B[i]/A[i][i];

 puts("Matrica D:");

 for(i=0;i<4;i++)

  printf("%f ",D[i]);

 printf(" \n");

 for(i=0;i<4;i++)

  X0[i]=D[i];

 max=1;

 while(max>=eps){

          max=0;

          for(i=0;i<4;i++)

           {X1[i]=C[i][0]*X0[0]+C[i][1]*X0[1]+C[i][2]*X0[2]+C[i][3]*X0[3]+D[i];

            if (fabs(X1[i]-X0[i])>max) max=fabs(X1[i]-X0[i]);

            X0[i]=X1[i]; }

                    }

 puts("X=");

 for(i=0;i<4;i++)

  printf("%f \n",X1[i]);

 getch();

}

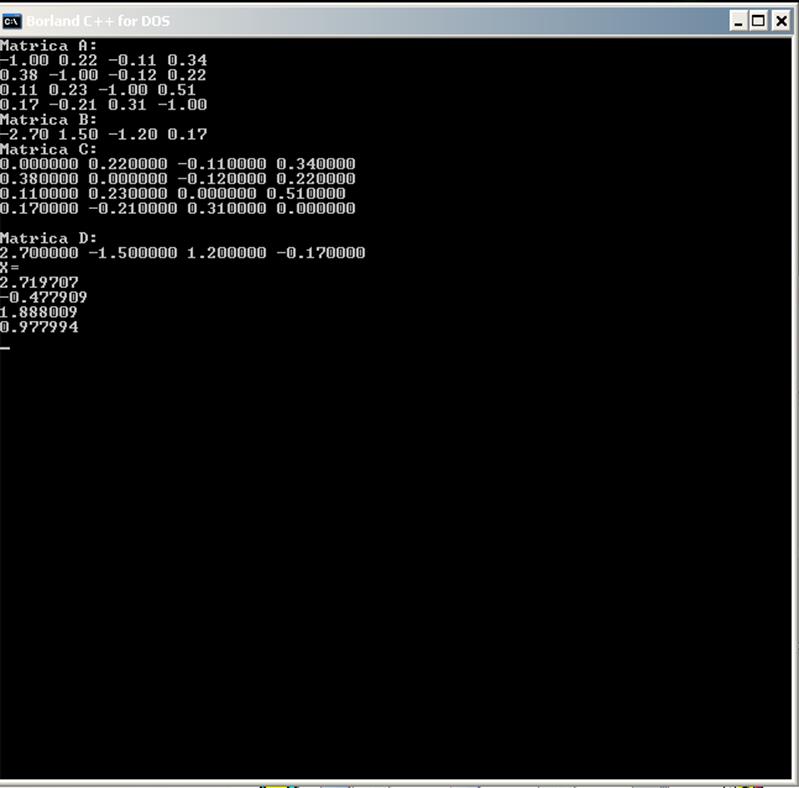
4. Пакетна реалізація

> with(linalg):

> solve( {-1.00*a+0.22*b-0.11*c+0.34*d=-2.7, 0.38*a-1.00*b-0.12*c+0.22*d=1.5, 0.11*a+0.23*b-1.00*c+0.51*d=-1.2, 0.17*a-0.21*b+0.31*c-1.00*d=0.17}, {a, b, c, d});

Висновки

В даній лабораторній роботі був виконаний розв’язок СЛАР з точнітю έ=0.0001.

Розв’язок був виконаний за допомогою пакету Maple, та програмно методом Зейделя за допомогою мови програмування С. Була визначена міра обумовленості матриці та зроблено оцінку похибки. Отримані дані свідчать про те, що вхідні дані були не досить точними, похибка складає близько 12%.

Значення отримані за допомогою пакету Maple та програмної реалізації метода Зейделя, збігаються, що свідчить про правильне розв’язання системи. Хоча ці значення отримані з певним наближенням.