|
I |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
|
0 1 2 3 4 |
1 32 40 9 |
6 28 35 13 |
36 4 5 37 |
11 24 30 17 |
25 21 16 20 |
27 3 14 38 |
39 18 2 23 |
29 26 12 15 |
10 33 31 8 |
19 34 22 7 |
|||
Тут номер рядка вказує число десятків, а номер стовпчика – число одиниць числа (індексу). У графі, спільній вказаним стовпчику та рядку, міститься відповідний індекс (число).
Наприклад, ind 25 знайдемо на перетині 2-го рядку з 5-м стовпчиком першої таблиці, тобто ind 25=4. Число, індекс якого 33 знайдемо в другій таблиці, на перетині третього рядку з третім стовпчиком, тобто 33 = ind17.
5. Наслідки попередньої теорії
a. Нехай p – просте непарне; α≥1, m – одне з чисел pα та p2α, c = φ(m).
b. Нехай (n,c) = d; тоді:
1. Конгруенція
xn = a(mod m); (a,m) = 1 (1)
розв`язується (і тим самим маємо лишок степеня n по модулю m)тоді і тільки тоді, коли ind a кратний d.
У випадку, якщо конгруенція розв`язується, вона має d рішень.
2.
В зведеній системі лишків
по модулю m число лишків степеня n є ![]() .
.
Дійсно, конгруенція (1) рівносильна наступній:
n ind x ≡ ind a(mod c) (2)
котра розв`язується тоді і тільки тоді, коли ind а кратний d.
Якщо (2) розв`язується, то ми можемо знайти d непорівнянних по модулю c значень для ind x; їм відповідає d непорівнянних по модулю m значень для x.
Таким чином вірно твердження 1.
Серед чисел 0, 1,
…. , c-1, які є найменшими
індексами лишків зведеної системи по модулю m, є ![]() кратних d. Отже твердження 2 вірне.
кратних d. Отже твердження 2 вірне.
Приклад 1. Для конгруенції
x3 ≡ 23(mod 41) (3)
маємо (8,40) = 8, причому ind 23 = 36не ділиться на 8. Значить (3) не розв`язується.
Приклад 2. Для конгруенції
x12 ≡37(mod 41) (4)
маємо (12, 40) = 4, причому ind 37 = 32 ділиться на 4. Значить (4) розв`язується і має 4 рішення.
Конгруенція (4) рівносильна наступним:
12 ind x ≡ 32(mod 40), ind x ≡ 6(mod 10)
Звідси для ind x знайдемо 4 непорівнянних по модулю 40 значення:
indx = 6, 16, 26, 36
Згідно чому знайдемо 4 розв`язки конгруенції (4)
x ≡ 39; 18; 2; 23(mod 41)
Приклад 3. Числа
1, 4, 10, 16, 18, 23, 25, 31, 37, 40 (5)
індекси котрих
рівні 4, це всі біквадратичні лишки (або всі лишки довільного степеня n = 4, 14, 28, …, де(n,40) = 4), серед найменших додатних лишків по модулю 41. Кількість
чисел з ряду (5) це 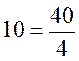 .
.
c. Число a є лишком степеня n по модулю m тоді і тільки тоді, коли
 (6)
(6)
Дійсно, умова ind a ≡ 0(modd) рівносильна ![]() ind a ≡ 0(modc). Останнє рівносильно умові (6).
ind a ≡ 0(modc). Останнє рівносильно умові (6).
Приклад. В теоремі пункту 3 неможливість конгруенції  рівносильна
умові, що g – нелишок степеня q по модулю m. Отже неможливість конгруенції
рівносильна
умові, що g – нелишок степеня q по модулю m. Отже неможливість конгруенції 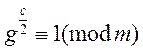 рівносильна
умові, що g–квадратичний нелишок
по модулю m.
рівносильна
умові, що g–квадратичний нелишок
по модулю m.
d.
1.
Показник δ, котрому a належить по модулю m, визначається рівністю (ind a, c) = ![]() ; належність
a до числа первісних коренів по модулю m визначається рівністю (ind a, c)=1.
; належність
a до числа первісних коренів по модулю m визначається рівністю (ind a, c)=1.
2. В зведеній системі лишків по модулю m число чисел, які належать показнику δ, є φ(δ), а число первісних коренів є φ(c).
Дійсно, δ - найменший дільник c з умовою aδ ≡ 1(mod m). Ця умова рівносильна
Δ ind a ≡ 0(mod c)
або
ind a ≡ 0(mod![]() )
)
Значить,δ – найменший дільникc, при якому ![]() ділить ind a, звідси
ділить ind a, звідси ![]() - найбільший дільник c, який ділить ind a, тобто
- найбільший дільник c, який ділить ind a, тобто ![]() =(ind a, c). Отже твердження 1 вірне.
=(ind a, c). Отже твердження 1 вірне.
Серед чисел 0, 1, …
, c-1, які є найменшими індексами
лишків зведеної системи по модулю m, кратними ![]() є числа виду
є числа виду ![]() , де y
= 0, 1, … , δ-1. Умова
, де y
= 0, 1, … , δ-1. Умова 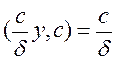 рівносильна умові (y, δ) = 1; останньому задовольняє φ(δ) значеньy. Отже твердження 2 вірне.
рівносильна умові (y, δ) = 1; останньому задовольняє φ(δ) значеньy. Отже твердження 2 вірне.
Приклад 1. В зведеній системі лишків по модулю 41 числами, які належать
показнику 10, є числа aз умовою (inda, 40) = ![]() =4, тобто числа
=4, тобто числа
4, 23, 25, 31.
Число цих чисел є 4 = φ(10).
Приклад 2. В зведеній системі лишків по модулю 41 первісними коренями є числа a з умовою (ind a, 40) = 1, тобто числа
6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35.
Число цих первісних коренів становить 16 = φ(40).
6. Індекси по модулю 2α
a. Для модулю 2α попередня теорія замінюється декілька більш складнішою.
b. Нехай α=1. Тоді 2α=2. Маємо φ(2)=1. Первісним коренем по модулю 2 буде, наприклад, 1≡-1(mod2). Число 10=(-1)0=1 створює зведену систему лишків по модулю 2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.